Zagadnienia
10. Całka względem ciągłych martyngałów
Podczas wcześniejszych wykładów zdefiniowaliśmy całkę ![]() . Okazuje się, że bez
większych trudności definicję tę daje się uogólnić na
. Okazuje się, że bez
większych trudności definicję tę daje się uogólnić na ![]() , gdzie
, gdzie ![]() jest ciągłym
martyngałem (a nawet ciągłym martyngałem lokalnym).
jest ciągłym
martyngałem (a nawet ciągłym martyngałem lokalnym).
10.1. Rozkład Dooba-Meyera
Podstawą konstrukcji całki stochastycznej względem procesu Wienera jest to, że ![]() i
i
![]() są martyngałami. Okazuje się, że dla dowolnego całkowalnego z kwadratem
ciągłego martyngału
są martyngałami. Okazuje się, że dla dowolnego całkowalnego z kwadratem
ciągłego martyngału ![]() znajdzie się proces niemalejący
znajdzie się proces niemalejący ![]() taki, że
taki, że ![]() jest
martyngałem.
jest
martyngałem.
Twierdzenie 10.1 (rozkład Dooba-Meyera)
Dla ![]() istnieje proces
istnieje proces ![]() o trajektoriach ciągłych, niemalejących taki, że
o trajektoriach ciągłych, niemalejących taki, że ![]() oraz
oraz
![]() jest martyngałem. Co więcej proces
jest martyngałem. Co więcej proces
![]() jest wyznaczony jednoznacznie.
jest wyznaczony jednoznacznie.
Udowodnimy jednoznaczność rozkładu, dowód istnienia można znaleźć w [5].
Dowód Jednoznaczności
Załóżmy, że procesy ![]() są
niemalejące oraz
są
niemalejące oraz ![]() i
i
![]() są martyngałami o ciągłych trajektoriach.
Trajektorie procesu
są martyngałami o ciągłych trajektoriach.
Trajektorie procesu ![]() mają wahanie skończone, ponadto
mają wahanie skończone, ponadto
![]() jest martyngałem ciągłym.
Stąd, na podstawie Twierdzenia 7.3,
jest martyngałem ciągłym.
Stąd, na podstawie Twierdzenia 7.3, ![]() .
.
Przykład 10.1
Dla procesu Wienera ![]() .
.
Ogólniej, Wniosek 9.1 implikuje, że ![]() dla
dla ![]() .
.
10.2. Całka izometryczna
Ponieważ dla wszystkich ![]() ,
, ![]() jest niemalejące, zatem ma wahanie skończone, czyli można określić skończoną miarę
jest niemalejące, zatem ma wahanie skończone, czyli można określić skończoną miarę
![]() na
na ![]() . Z uwagi na ciągłość
. Z uwagi na ciągłość ![]() miara
ta jest bezatomowa. Następna definicja jest naturalnym uogólnieniem
definicji dla procesu Wienera.
miara
ta jest bezatomowa. Następna definicja jest naturalnym uogólnieniem
definicji dla procesu Wienera.
Definicja 10.1
Dla procesu elementarnego ![]() postaci
postaci
![X=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{{k=0}}^{{m-1}}\xi _{k}{\mathrm{I}}_{{(t_{k},t_{{k+1}}]}},](wyklady/was/mi/mi1462.png) |
gdzie ![]() ,
,
![]() ograniczone,
ograniczone, ![]() - mierzalne oraz
- mierzalne oraz ![]() określamy
określamy
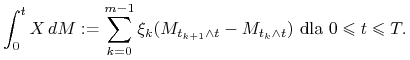 |
Definiujemy też dla ![]() ,
,
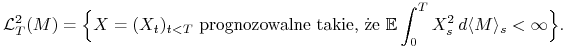 |
Stwierdzenie 10.1
Niech ![]() oraz
oraz ![]() . Wówczas
. Wówczas
![]() ,
, ![]() oraz
oraz
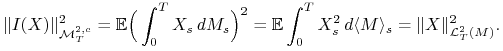 |
Ciągłość ![]() , warunek
, warunek
![]() oraz to, że
oraz to, że ![]() dla wszystkich
dla wszystkich ![]() są oczywiste.
Dla
są oczywiste.
Dla ![]() mamy
mamy
Dla ![]() otrzymujemy zatem
otrzymujemy zatem
czyli ![]() jest martyngałem. Ponadto
jest martyngałem. Ponadto
![\displaystyle\sum _{{k=0}}^{{m-1}}{\mathbb{E}}[\xi _{k}^{2}(M_{{t_{{k+1}}}}-M_{{t_{k}}})^{2}]](wyklady/was/mi/mi1415.png) |
|||
Zauważmy, że dla ![]() ,
,
Stąd
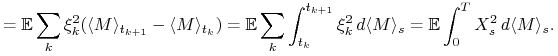 |
Ponadto
Tak jak dla procesu Wienera dowodzimy, że domknięcie ![]() w przestrzeni
w przestrzeni
![]() jest równe
jest równe
![]() .
Izometrię
.
Izometrię ![]() możemy przedłużyć do
możemy przedłużyć do ![]() ,
w ten sposób otrzymujemy izometryczną definicję całki
,
w ten sposób otrzymujemy izometryczną definicję całki
![]() dla
dla ![]() . Mamy zatem następujący fakt.
. Mamy zatem następujący fakt.
Stwierdzenie 10.2
Niech ![]() . Wówczas
. Wówczas
a) Dla ![]() proces
proces ![]() oraz
oraz
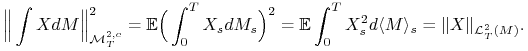 |
b) Jeśli ![]() , to
, to ![]() dla
dla ![]() oraz
oraz ![]() .
.
10.3. Uogólnienie definicji całki
Zacznijmy od prostego faktu.
Stwierdzenie 10.3
Załóżmy, że ![]() , wówczas dla dowolnego momentu zatrzymania
, wówczas dla dowolnego momentu zatrzymania ![]() ,
,
![]() oraz
oraz ![]() .
.
Wiemy, że ![]() jest ciągłym martyngałem. Na mocy nierówności Jensena
jest ciągłym martyngałem. Na mocy nierówności Jensena
zatem ![]() . Proces
. Proces ![]() startuje z zera,
ma trajektorie ciągłe, ponadto
startuje z zera,
ma trajektorie ciągłe, ponadto ![]() jest martyngałem, więc
jest martyngałem, więc ![]() spełnia
wszystkie warunki definicji
spełnia
wszystkie warunki definicji ![]() .
.
Możemy uogólnić rozkład Dooba-Meyera na przypadek ciągłych martyngałów lokalnych.
Wniosek 10.1
Załóżmy, że ![]() , wówczas istnieje dokładnie jeden proces
, wówczas istnieje dokładnie jeden proces
![]() o trajektoriach ciągłych, niemalejących taki, że
o trajektoriach ciągłych, niemalejących taki, że ![]() oraz
oraz
![]() .
.
Istnienie. Niech ![]() będzie rosnącym do
będzie rosnącym do ![]() ciągiem momentów zatrzymania
takim, że
ciągiem momentów zatrzymania
takim, że ![]() . Określmy
. Określmy ![]() ,
wówczas dla
,
wówczas dla ![]() ,
,
Stąd istnieje proces ciągły ![]() taki, że
taki, że ![]() ,
oczywiście
,
oczywiście ![]() , ponadto
, ponadto ![]() ma trajektorie niemalejące oraz
ma trajektorie niemalejące oraz
zatem ![]() jest ciągłym martyngałem lokalnym na
jest ciągłym martyngałem lokalnym na ![]() .
.
Jednoznaczność. Niech ![]() i
i ![]() procesy ciągłe o niemalejących trajektoriach
takie, że
procesy ciągłe o niemalejących trajektoriach
takie, że ![]() oraz
oraz
![]() i
i ![]() są martyngałami lokalnymi. Wówczas istnieją momenty zatrzymania
są martyngałami lokalnymi. Wówczas istnieją momenty zatrzymania ![]() i
i ![]() takie, że
takie, że ![]() oraz
oraz ![]() są
martyngałami. Biorąc
są
martyngałami. Biorąc ![]() dostajemy martyngały
dostajemy martyngały
![]() oraz
oraz
![]() , proces
, proces
![]() jest więc martyngałem o ograniczonym wahaniu, czyli jest stały,
zatem
jest więc martyngałem o ograniczonym wahaniu, czyli jest stały,
zatem ![]() . Przechodząc z
. Przechodząc z ![]() otrzymujemy
otrzymujemy
![]()
Podobnie jak dla procesu Wienera dowodzimy twierdzenie o zatrzymaniu całki stochastycznej względem martyngałów całkowalnych z kwadratem.
Twierdzenie 10.2
Załóżmy, że ![]() ,
, ![]() oraz
oraz ![]() jest momentem zatrzymania.
Wówczas
jest momentem zatrzymania.
Wówczas ![]() ,
, ![]() oraz
oraz
Definicja 10.2
Dla ![]() ,
, ![]() określamy przestrzeń procesów prognozowalnych, lokalnie całkowalnych
z kwadratem względem
określamy przestrzeń procesów prognozowalnych, lokalnie całkowalnych
z kwadratem względem ![]()
Ponieważ ![]() oraz
oraz ![]() ,
więc bez straty ogólności przy uogólnianiu definicji całki będziemy zakładać, że
,
więc bez straty ogólności przy uogólnianiu definicji całki będziemy zakładać, że
![]() .
.
Definicja 10.3
Niech ![]() ,
, ![]() ,
, ![]() oraz
oraz
![]() będzie rosnącym do
będzie rosnącym do ![]() ciągiem momentów zatrzymania
takich, że
ciągiem momentów zatrzymania
takich, że ![]() i
i ![]() dla wszystkich
dla wszystkich ![]() .
Całką stochastyczną
.
Całką stochastyczną
![]() nazywamy taki
proces
nazywamy taki
proces ![]() , że
, że
![]() dla
dla ![]() .
.
Nietrudno udowodnić (naśladując dowód dla całki względem procesu Wienera), że
całka ![]() dla
dla ![]() i
i ![]() jest zdefiniowana
poprawnie i jednoznacznie (z dokładnością do nieodróżnialności procesów) oraz nie zależy
od wyboru ciągu momentów zatrzymania
jest zdefiniowana
poprawnie i jednoznacznie (z dokładnością do nieodróżnialności procesów) oraz nie zależy
od wyboru ciągu momentów zatrzymania ![]() .
.
Następujący fakt przedstawia podstawowe własności ![]() .
.
Stwierdzenie 10.4
Niech ![]() . Wówczas
. Wówczas
a) Dla ![]() proces
proces ![]() .
.
b) Jeśli ![]() , to
, to ![]() dla
dla ![]() oraz
oraz ![]() .
.
c) Jeśli ![]() oraz
oraz ![]() , to
, to ![]() oraz
oraz ![]() .
.
Można również sformułować twierdzenie o zatrzymaniu całki stochastycznej w ogólnym przypadku.
Twierdzenie 10.3
Załóżmy, że ![]() ,
, ![]() oraz
oraz ![]() będzie momentem zatrzymania.
Wówczas
będzie momentem zatrzymania.
Wówczas ![]() ,
, ![]() oraz
oraz
10.4. Zadania
Ćwiczenie 10.1
Niech ![]() . Oblicz
. Oblicz ![]() . Jak wygląda przestrzeń
. Jak wygląda przestrzeń ![]() ?
Czy
?
Czy ![]() należy do tej przestrzeni?
należy do tej przestrzeni?
Ćwiczenie 10.3
Udowodnij Stwierdzenie 10.4.
Ćwiczenie 10.4
Załóżmy, że ![]() jest procesem ciągłym, a
jest procesem ciągłym, a ![]() ciągłym martyngałem lokalnym. Wykaż, że
jeśli
ciągłym martyngałem lokalnym. Wykaż, że
jeśli ![]() ,
,
![]() jest ciągiem podziałów
jest ciągiem podziałów ![]() takim, że
takim, że ![]() oraz
oraz
![]() , to
, to
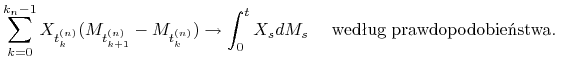 |
Ćwiczenie 10.5
Wykaż, że każdy ciągły martyngał lokalny ![]() ,
którego trajektorie mają skończone wahanie na każdym przedziale
,
którego trajektorie mają skończone wahanie na każdym przedziale ![]() jest stale
równy
jest stale
równy ![]() .
.




