Zagadnienia
4. Filtracje, momenty zatrzymania
Pokażemy jak zmodyfikować definicje omawiane podczas kursowego wykładu z rachunku prawdopodobieństwa z przypadku czasu dyskretnego na czas ciągły.
Będziemy zakładać, że ![]() jest lewostronnie domkniętym przedziałem (typowo
jest lewostronnie domkniętym przedziałem (typowo ![]() ),
choć większość definicji i wyników można uogólnić na szerszą klasę zbiorów.
),
choć większość definicji i wyników można uogólnić na szerszą klasę zbiorów.
4.1. Filtracje z czasem ciągłym
Definicja 4.1
Filtracją![]() przestrzeni probabilistycznej
przestrzeni probabilistycznej
![]() nazywamy rosnącą rodzinę
nazywamy rosnącą rodzinę ![]() -ciał zawartych w
-ciał zawartych w ![]() ,
tzn.
,
tzn. ![]() dla
dla ![]() .
.
Zdarzenia z ![]() -ciała
-ciała ![]() możemy interpretować jako zdarzenia obserwowalne do
chwili
możemy interpretować jako zdarzenia obserwowalne do
chwili ![]() .
.
Definicja 4.2
Niech ![]() będzie procesem stochastycznym. Filtracją generowaną przez
będzie procesem stochastycznym. Filtracją generowaną przez
![]() nazywamy rodzinę
nazywamy rodzinę ![]() daną wzorem
daną wzorem
![]() .
.
Stwierdzenie 4.1
Proces ![]() ma przyrosty niezależne wtedy i tylko wtedy, gdy dla dowolnych
ma przyrosty niezależne wtedy i tylko wtedy, gdy dla dowolnych ![]() ,
, ![]() przyrost
przyrost ![]() jest niezależny od
jest niezależny od ![]() -ciała
-ciała ![]() .
.
![]() : Rodzina
: Rodzina ![]() zdarzeń niezależnych od
zdarzeń niezależnych od ![]() tworzy
tworzy
![]() -układ, ponadto,
z niezależności przyrostów
-układ, ponadto,
z niezależności przyrostów ![]() , zawiera
, zawiera ![]() -układ zdarzeń postaci
-układ zdarzeń postaci
![]() dla
dla ![]() , który generuje
, który generuje ![]() -ciało
-ciało
![]() . Zatem, na mocy twierdzenia o
. Zatem, na mocy twierdzenia o ![]() - i
- i ![]() -układach,
-układach,
![]() .
.
![]() : Ustalmy
: Ustalmy ![]() oraz zbiory borelowskie
oraz zbiory borelowskie ![]() . Zdarzenie
. Zdarzenie
![]() należy
do
należy
do ![]() -ciała
-ciała ![]() , więc jest niezależne od zmiennej
, więc jest niezależne od zmiennej ![]() .
Stąd
.
Stąd
Iterując to rozumowanie pokazujemy, że
Definicja 4.3
Proces ![]() nazywamy zgodnym z filtracją
nazywamy zgodnym z filtracją ![]() ,
,
![]() -adaptowalnym lub adaptowanym do filtracji
-adaptowalnym lub adaptowanym do filtracji ![]() ,
jeśli dla wszystkich
,
jeśli dla wszystkich ![]() ,
, ![]() jest
jest ![]() mierzalne.
mierzalne.
Uwaga 4.1
Oczywiście proces ![]() jest zgodny z filtracją
jest zgodny z filtracją ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
![]() dla
dla ![]() . W szczególności
każdy proces
. W szczególności
każdy proces ![]() jest zgodny z filtracją przez siebie generowaną.
jest zgodny z filtracją przez siebie generowaną.
4.2. Momenty zatrzymania
Definicja 4.4
Momentem zatrzymania (momentem Markowa, czasem zatrzymania) względem filtracji
![]() nazywamy zmienną losową o wartościach w
nazywamy zmienną losową o wartościach w ![]() taką, że
taką, że
![]() dla wszystkich
dla wszystkich ![]() .
.
Moment zatrzymania to strategia przerwania eksperymentu losowego (np.
zakończenia udziału w pewnej grze losowej) taka, że decyzję o przerwaniu do chwili ![]() podejmujemy
tylko na podstawie obserwacji dostępnych w tym czasie.
podejmujemy
tylko na podstawie obserwacji dostępnych w tym czasie.
Dla zbioru ![]() i procesu stochastycznego
i procesu stochastycznego ![]() określmy
określmy
Stwierdzenie 4.2
Jeśli ![]() jest
jest ![]() -adaptowalnym procesem o ciągłych trajektoriach, zaś
-adaptowalnym procesem o ciągłych trajektoriach, zaś
![]() zbiorem domkniętym, to
zbiorem domkniętym, to
![]() jest momentem zatrzymania względem filtracji
jest momentem zatrzymania względem filtracji ![]() .
.
Niech ![]() będzie gęstym podzbiorem
będzie gęstym podzbiorem ![]() zawierającym lewy
koniec. Z domkniętości zbioru
zawierającym lewy
koniec. Z domkniętości zbioru ![]() i ciągłości
i ciągłości ![]() dostajemy dla
dostajemy dla ![]() ,
,
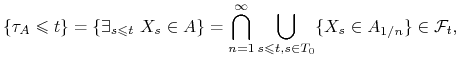 |
gdzie
Uwaga 4.2
Jeśli w powyższym przykładzie ![]() będzie zbiorem otwartym, to
będzie zbiorem otwartym, to ![]() nie musi być
momentem zatrzymania względem filtracji
nie musi być
momentem zatrzymania względem filtracji ![]() , ale musi być momentem
zatrzymania względem filtracji
, ale musi być momentem
zatrzymania względem filtracji ![]() , gdzie dla
, gdzie dla ![]()
a jeśli ![]() jest największym elementem
jest największym elementem ![]() , to kładziemy
, to kładziemy ![]() .
.
Powyższa uwaga motywuje poniższą definicję, która ma nieco techniczny charakter, ale jest powszechnie używana w teorii procesów.
Definicja 4.5
Filtrację ![]() nazywamy prawostronnie ciągłą, jeśli
nazywamy prawostronnie ciągłą, jeśli
![]() dla wszystkich
dla wszystkich ![]() . Mówimy, że filtracja
. Mówimy, że filtracja
![]() spełnia zwykłe warunki, jeśli
spełnia zwykłe warunki, jeśli
a) jest prawostronnie ciągła,
b) dla wszystkich ![]() ,
, ![]() zawiera wszystkie zbiory miary zero, tzn.
jeśli
zawiera wszystkie zbiory miary zero, tzn.
jeśli ![]() ,
, ![]() , to
, to ![]() .
.
Definicja 4.6
Niech ![]() będzie momentem zatrzymania względem filtracji
będzie momentem zatrzymania względem filtracji ![]() .
Definiujemy
.
Definiujemy ![]() -ciało zdarzeń obserwowalnych do chwili
-ciało zdarzeń obserwowalnych do chwili ![]() wzorem
wzorem
Stwierdzenie 4.3
a) Zbiór ![]() jest
jest ![]() -ciałem.
-ciałem.
b) Jeśli ![]() , to
, to ![]() .
.
c) Zmienna losowa ![]() jest
jest ![]() mierzalna.
mierzalna.
a) Zbiór ![]() , bo
, bo ![]() . Jeśli
. Jeśli
![]() , to
, to ![]() , czyli
, czyli ![]() . Jeśli
. Jeśli ![]() , to
, to
![]() ,
zatem
,
zatem ![]() .
.
b) Weźmy ![]() , wówczas dla
, wówczas dla ![]() ,
, ![]() , czyli
, czyli ![]() .
.
c) Wystarczy pokazać, że ![]() , ale
, ale
![]() .
.
Stwierdzenie 4.4
Załóżmy, że ![]() i
i ![]() są momentami zatrzymania. Wówczas
są momentami zatrzymania. Wówczas ![]() oraz zdarzenia
oraz zdarzenia ![]() należą do
należą do ![]() .
.
Zauważmy, że ![]() jest momentem zatrzymania oraz
jest momentem zatrzymania oraz
![]() i
i ![]() , zatem na mocy
Stwierdzenia 4.3 dostajemy
, zatem na mocy
Stwierdzenia 4.3 dostajemy ![]() . Na odwrót, jeśli
. Na odwrót, jeśli ![]() , to
, to
![]() , czyli
, czyli
![]() . Dalszą część stwierdzenia pozostawiamy do samodzielnego udowodnienia w ramach prostego ćwiczenia.
. Dalszą część stwierdzenia pozostawiamy do samodzielnego udowodnienia w ramach prostego ćwiczenia.
4.3. Progresywna mierzalność
Okazuje się, że adaptowalność procesu nie gwarantuje np. mierzalności zmiennych ![]() dla wszystkich momentów zatrzymania
dla wszystkich momentów zatrzymania ![]() . Dlatego wprowadzimy jeszcze jedną techniczną
definicję.
. Dlatego wprowadzimy jeszcze jedną techniczną
definicję.
Definicja 4.7
Proces ![]() nazywamy progresywnie mierzalnym względem filtracji
nazywamy progresywnie mierzalnym względem filtracji
![]() , jeśli dla każdego
, jeśli dla każdego ![]() , funkcja
, funkcja ![]() traktowana jako funkcja ze zbioru
traktowana jako funkcja ze zbioru ![]() w
w ![]() jest mierzalna
względem
jest mierzalna
względem ![]() -algebry
-algebry ![]() . Równoważnie
. Równoważnie
Stwierdzenie 4.5
Załóżmy, że ![]() jest przedziałem oraz dany jest proces
jest przedziałem oraz dany jest proces ![]() oraz
filtracja
oraz
filtracja ![]() .
.
a) Jeśli proces ![]() jest progresywnie mierzalny względem
jest progresywnie mierzalny względem ![]() , to
jest
, to
jest ![]() -adaptowalny.
-adaptowalny.
b) Jeśli proces ![]() jest
jest ![]() -adaptowalny oraz ma prawostronnie ciągłe trajektorie,
to jest progresywnie mierzalny względem
-adaptowalny oraz ma prawostronnie ciągłe trajektorie,
to jest progresywnie mierzalny względem ![]() .
.
a) Zbiór ![]() jest przekrojem zbioru
jest przekrojem zbioru
![]() , a zatem należy do
, a zatem należy do ![]() .
.
b) Ustalmy ![]() i połóżmy dla
i połóżmy dla ![]() ,
, ![]() ,
, ![]() , gdzie
, gdzie
![]() jest liczbą całkowitą taką, że
jest liczbą całkowitą taką, że ![]() . Wówczas
. Wówczas
![\displaystyle=\bigcup _{{k=0}}^{{\infty}}\Big(T\cap\Big(t-\frac{k+1}{2^{{n}}},t-\frac{k}{2^{{n}}}\Big]\Big)\times\{\omega\colon X_{{t-\frac{k}{2^{{n}}}}}(\omega)\in A\}](wyklady/was/mi/mi385.png) |
|||
Zatem funkcja ![]() jest
jest
![]() mierzalna. Wobec prawostronnej ciągłości
mierzalna. Wobec prawostronnej ciągłości ![]() mamy
mamy
![]() , więc funkcja
, więc funkcja
![]() jest
jest
![]() mierzalna jako granica funkcji mierzalnych.
mierzalna jako granica funkcji mierzalnych.
Jeśli ![]() jest momentem zatrzymania, a
jest momentem zatrzymania, a ![]() procesem, to zmienna
procesem, to zmienna ![]() jest dobrze zdefiniowana tylko na zbiorze
jest dobrze zdefiniowana tylko na zbiorze ![]() . Musimy zatem określić co mamy
na myśli mówiąc, że zmienna
. Musimy zatem określić co mamy
na myśli mówiąc, że zmienna ![]() jest mierzalna.
jest mierzalna.
Definicja 4.8
Mówimy, że zmienna losowa ![]() określona na zbiorze
określona na zbiorze ![]() jest mierzalna względem
jest mierzalna względem ![]() -ciała
-ciała
![]() zawierającego
zawierającego ![]() , jeśli
, jeśli ![]() dla
dowolnego zbioru borelowskiego
dla
dowolnego zbioru borelowskiego ![]() .
.
Przed sformułowaniem kolejnego stwierdzenia wprowadzimy jeszcze jedną użyteczną definicję.
Definicja 4.9
Jeśli ![]() jest procesem stochastycznym, a
jest procesem stochastycznym, a ![]() zmienną o wartościach w
zmienną o wartościach w
![]() , to definujemy
, to definujemy ![]() – proces
– proces ![]() zatrzymany
w czasie
zatrzymany
w czasie ![]() wzorem
wzorem ![]() .
.
Stwierdzenie 4.6
Załóżmy, że ![]() jest procesem progresywnie mierzalnym względem filtracji
jest procesem progresywnie mierzalnym względem filtracji
![]() , a
, a ![]() jest momentem zatrzymania. Wówczas zmienna losowa
jest momentem zatrzymania. Wówczas zmienna losowa
![]() określona na zbiorze
określona na zbiorze ![]() jest
jest ![]() mierzalna. Ponadto
mierzalna. Ponadto ![]() – proces
– proces ![]() zatrzymany w chwili
zatrzymany w chwili ![]() jest progresywnie mierzalny.
jest progresywnie mierzalny.
Odwzorowanie
jest mierzalne względem ![]() -ciała
-ciała ![]() .
Jeśli złożymy je z odwzorowaniem
.
Jeśli złożymy je z odwzorowaniem
to otrzymamy odwzorowanie
Stąd wynika progresywna mierzalność procesu ![]() . By zakończyć dowód zauważmy, że
. By zakończyć dowód zauważmy, że
na mocy progresywnej mierzalności (a właściwie adaptowalności) ![]() .
.
4.4. Zadania
Ćwiczenie 4.1
Załóżmy, że ![]() jest przedziałem i określmy:
jest przedziałem i określmy:
a) Wykaż, że filtracja ![]() jest prawostronnie ciągła, tzn.
jest prawostronnie ciągła, tzn. ![]() .
.
b) Udowodnij, że jeśli ![]() jest filtracją generowaną przez
proces
jest filtracją generowaną przez
proces ![]() o lewostronnie ciągłych trajektoriach, to
o lewostronnie ciągłych trajektoriach, to ![]() .
.
c) Niech ![]() oraz
oraz ![]() . Znajdź
. Znajdź ![]() .
.
d) Dla ![]() jak w punkcie c) określmy
jak w punkcie c) określmy ![]() . Wykaż, że
. Wykaż, że ![]() nie jest momentem zatrzymania względem
nie jest momentem zatrzymania względem ![]() ale jest momentem zatrzymania
względem
ale jest momentem zatrzymania
względem ![]() .
.
Ćwiczenie 4.2
Załóżmy, że ![]() jest przedziałem, wykaż, że:
jest przedziałem, wykaż, że:
a) jeśli ![]() jest momentem zatrzymania, to
jest momentem zatrzymania, to ![]() dla wszystkich
dla wszystkich ![]() ;
;
b) jeśli ![]() dla wszystkich
dla wszystkich ![]() , to
, to ![]() jest momentem zatrzymania
względem
jest momentem zatrzymania
względem ![]() .
.
Ćwiczenie 4.3
Niech ![]() , a
, a ![]() będzie momentem zatrzymania, które ze zmiennych
będzie momentem zatrzymania, które ze zmiennych
![]() muszą być momentami zatrzymania?
muszą być momentami zatrzymania?
Ćwiczenie 4.4
Niech ![]() , a
, a ![]() procesem
procesem ![]() -adaptowalnym o ciągłych
trajektoriach. Wykaż, że dla
-adaptowalnym o ciągłych
trajektoriach. Wykaż, że dla ![]() otwartego
otwartego ![]() jest momentem zatrzymania względem
jest momentem zatrzymania względem ![]() .
.
Ćwiczenie 4.5
Wykaż, że jeśli ![]() i
i ![]() są momentami zatrzymania, to zdarzenia
są momentami zatrzymania, to zdarzenia
![]() i
i ![]() należą do
należą do
![]() ,
, ![]() i
i ![]() .
.
Ćwiczenie 4.6
Wykaż, że jeśli ![]() jest momentem zatrzymania, to proces
jest momentem zatrzymania, to proces ![]() jest progresywnie mierzalny.
jest progresywnie mierzalny.
Ćwiczenie 4.7
Niech ![]() będzie momentem zatrzymania względem
będzie momentem zatrzymania względem ![]() ,
a
,
a ![]() będzie procesem
będzie procesem ![]() -adaptowalnym. Wykaż, że
-adaptowalnym. Wykaż, że
a) ![]() jest
jest ![]() -mierzalne;
-mierzalne;
b) jeśli ![]() przyjmuje przeliczalnie wiele wartości, to
przyjmuje przeliczalnie wiele wartości, to ![]() jest
jest ![]() mierzalny na zbiorze
mierzalny na zbiorze ![]() .
.
Ćwiczenie 4.8
Wykaż, że jeśli ![]() jest momentem zatrzymania,
jest momentem zatrzymania, ![]() oraz
oraz
![]() jest
jest ![]() mierzalny, to
mierzalny, to ![]() jest momentem zatrzymania.
jest momentem zatrzymania.
Ćwiczenie 4.9
Wykaż, że jeśli proces ![]() ma niezależne przyrosty i prawostronnie ciągłe trajektorie,
to dla
ma niezależne przyrosty i prawostronnie ciągłe trajektorie,
to dla ![]() zmienna
zmienna ![]() jest niezależna od
jest niezależna od ![]() .
.




