Zagadnienia

13.1 Podstawowe twierdzenie analizy stochastycznej
13.2 Twierdzenie Levy'ego
13.3 Charakteryzacja procesu Wienera za pomocą martyngałów wykładniczych
13.4 Zadania

13. Wzór Itô

Podczas tego wykładu udowodnimy fundamentalne twierdzenie dla analizy stochastycznej. Pokazuje ono, że klasa semimartyngałów ciągłych jest zamknięta ze względu na funkcje gładkie oraz podaje wzór na różniczkę stochastyczną $df(X)$ .

13.1. Podstawowe twierdzenie analizy stochastycznej

Twierdzenie 13.1 (Wzór Itô)

Załóżmy, że $Z=Z_{0}+M+A$ jest ciągłym semimartyngałem, $f$ funkcją klasy $C^{2}$ na ${\mathbb{R}}$ . Wówczas $f(Z)$ też jest semimartyngałem oraz

$f(Z_{t})=f(Z_{0})+\int _{0}^{t}f^{{\prime}}(Z_{s})dZ_{s}+\frac{1}{2}\int _{0}^{t}f^{{\prime\prime}}(Z_{s})d\langle M\rangle _{s}.$

(13.1)

Wszystkie całki w (13.1) są dobrze zdefiniowane, bo procesy $f^{{\prime}}(Z_{s})$ i $f^{{\prime\prime}}(Z_{s})$ są ciągłe, zatem $f^{{\prime}}(Z_{s})\in\Lambda^{2}_{T}(M)$ oraz $f^{{\prime\prime}}(Z_{s})$ jest całkowalne względem $\langle M\rangle$ .

Wzór Itô (13.1) będziemy dowodzić poczynając od najprostszych przypadków.

Przypadek I. $Z$ jest semimartyngałem ograniczonym, a $f$ wielomianem.

Z liniowości obu stron (13.1) wystarczy rozpatrywać przypadek, gdy $f(x)=x^{n}$ . Pokażemy ten wzór przez indukcję po $n$ .

Dla $n=0$ teza jest oczywista. Załóżmy więc, że (13.1) zachodzi dla $f(x)=x^{n}$ pokażemy go dla $g(x)=xf(x)$ . Zauważmy, że $g^{{\prime}}(x)=f(x)+xf^{{\prime}}(x)$ oraz $g^{{\prime\prime}}(x)=2f^{{\prime}}(x)+xf^{{\prime\prime}}(x)$ . Ze wzoru na całkowanie przez części,

	$\displaystyle g(Z_{t})=$	$\displaystyle Z_{t}f(Z_{t})=Z_{0}f(Z_{0})+\int _{0}^{t}Z_{s}df(Z)_{s}+\int _{0}^{t}f(Z)dZ_{s}$
		$\displaystyle+\Big\langle\int f^{{\prime}}(Z)dM,M\Big\rangle _{t}$
	$\displaystyle=$	$\displaystyle g(Z_{t})+\int _{0}^{t}(Z_{s}f^{{\prime}}(Z_{s})dZ_{s}+\frac{1}{2}Z_{s}f^{{\prime\prime}}(Z_{s})d\langle M\rangle _{s})+\int _{0}^{t}f(Z)dZ_{s}$
		$\displaystyle+\int _{0}^{t}f^{{\prime}}(Z_{s})d\langle M\rangle _{s}$
	$\displaystyle=$	$\displaystyle g(Z_{t})+\int _{0}^{t}g^{{\prime}}(Z_{t})dZ_{t}+\frac{1}{2}\int _{0}^{t}g^{{\prime\prime}}(Z_{t})d\langle M\rangle _{s}.$

Przypadek II. $Z$ jest semimartyngałem ograniczonym (a $f$ jest dowolną funkcją klasy $C^{2}$ ).

Niech $C:=\| Z\| _{{\infty}}<\infty$ , istnieje ciąg wielomianów $f_{n}$ taki, że

$|f_{n}(x)-f(x)|,|f_{n}^{{\prime}}(x)-f^{{\prime}}(x)|,|f_{n}^{{\prime\prime}}(x)-f^{{\prime\prime}}(x)|\leq\frac{1}{n}\quad\mbox{dla }x\in[-C,C].$

Wtedy $f_{n}(Z_{s})\rightarrow f(Z_{s}),f_{n}^{{\prime}}(Z_{s})\rightarrow f^{{\prime}}(Z_{s}),f_{n}^{{\prime\prime}}(Z_{s})\rightarrow f^{{\prime\prime}}(Z_{s})$ jednostajnie oraz $|f_{n}^{{\prime}}(Z_{s})|\leq\sup _{n}\sup _{{|x|\leq C}}|f_{n}^{{\prime}}(x)|\leq\sup _{{|x|\leq C}}|f^{{\prime}}(x)|+1<\infty$ , więc z twierdzenia Lebesgue'a o zbieżności zmajoryzowanej (dla całki zwykłej i stochastycznej),

	$\displaystyle f(Z_{s})\leftarrow f_{n}(Z_{s})$	$\displaystyle=f_{n}(Z_{0})+\int _{0}^{t}f_{n}^{{\prime}}(Z_{s})dZ_{s}+\frac{1}{2}\int _{0}^{t}f_{n}^{{\prime\prime}}(Z_{s})d\langle M\rangle _{s}$
		$\displaystyle\rightarrow f(Z_{0})+\int _{0}^{t}f^{{\prime}}(Z_{s})dZ_{s}+\frac{1}{2}\int _{0}^{t}f^{{\prime\prime}}(Z_{s})d\langle M\rangle _{s}.$

Przypadek III. Zmienna $Z_{0}$ jest ograniczona.

Połóżmy w tym przypadku

$\tau _{n}:=\inf\{ t>0\colon|Z_{t}|\geq n\}\wedge T,$

wówczas $Z^{{(n)}}:=Z_{0}+M^{{\tau _{n}}}+A^{{\tau _{n}}}$ jest ciągłym ograniczonym semimartyngałem oraz $Z^{{(n)}}_{t}\rightarrow Z_{t}$ p.n.. Na mocy przypadku II, (13.1) zachodzi dla $Z^{{(n)}}$ , więc

	$\displaystyle f(Z^{{(n)}}_{t})$	$\displaystyle=f(Z_{0})+\int _{0}^{t}f^{{\prime}}(Z^{{(n)}}_{s})dZ^{{(n)}}_{s}+\frac{1}{2}\int _{0}^{t}f^{{\prime\prime}}(Z_{s}^{{(n)}})d\langle M^{{\tau _{n}}}\rangle _{s}$
		$\displaystyle=f(Z_{0})+\int _{0}^{{t\wedge\tau _{n}}}f^{{\prime}}(Z^{{(n)}}_{s}){\mathrm{I}}_{{[0,\tau _{n}]}}dZ_{s}+\frac{1}{2}\int _{0}^{{t\wedge\tau _{n}}}f^{{\prime\prime}}(Z_{s}^{{(n)}}){\mathrm{I}}_{{[0,\tau _{n}]}}d\langle M\rangle _{s}^{{\tau _{n}}}$
		$\displaystyle=f(Z_{0})+\int _{0}^{{t\wedge\tau _{n}}}f^{{\prime}}(Z_{s}){\mathrm{I}}_{{[0,\tau _{n}]}}dZ_{s}+\frac{1}{2}\int _{0}^{{t\wedge\tau _{n}}}f^{{\prime\prime}}(Z_{s}){\mathrm{I}}_{{[0,\tau _{n}]}}d\langle M\rangle _{s}$
		$\displaystyle=f(Z_{0})+\int _{0}^{{t\wedge\tau _{n}}}f^{{\prime}}(Z_{s})dZ_{s}+\frac{1}{2}\int _{0}^{{t\wedge\tau _{n}}}f^{{\prime\prime}}(Z_{s})d\langle M\rangle _{s}.$

Biorąc $n\rightarrow\infty$ dostajemy (13.1).

Przypadek IV. $Z$ jest dowolnym semimartyngałem ciągłym.

Połóżmy $Z_{0}^{{(n)}}:=(Z_{0}\wedge n)\vee-n$ oraz $Z^{{(n)}}:=Z_{0}^{{(n)}}+M+A$ . Zauważmy, że $\int XdZ=\int XdZ^{{(n)}}$ , więc, ponieważ wiemy już, iż (13.1) zachodzi, gdy $Z_{0}$ ograniczone, to

$f(Z_{t}^{{(n)}})=f(Z_{0}^{{(n)}})+\int _{0}^{t}f^{{\prime}}(Z_{s}^{{(n)}})dZ_{s}+\frac{1}{2}\int _{0}^{t}f^{{\prime\prime}}(Z_{s}^{{(n)}})d\langle M\rangle _{s}.$

(13.2)

Mamy

$|f^{{\prime}}(Z_{s}^{{(n)}})|\leq\sup _{n}|f^{{\prime}}(Z_{s}^{{(n)}})|:=Y_{s},$

proces $Y$ jest prognozowalny jako supremum procesów prognozowalnych, ponadto

$\sup _{n}\sup _{{s\leq t}}|Z_{s}^{{(n)}}|\leq|Z_{0}|+\sup _{{s\leq t}}|M_{s}|+\sup _{{s\leq t}}|A_{s}|<\infty\mbox{ p.n..}$

Zatem z ciągłości $f^{{\prime}}$ , $\sup _{{s\leq t}}|Y_{s}|<\infty$ p.n., skąd $Y\in\Lambda _{T}^{2}(M)$ . Z twierdzenia Lebesgue'a o zbieżności zmajoryzowanej dla całek stochastycznych,

$\int _{0}^{t}f^{{\prime}}(Z_{s}^{{(n)}})dM_{s}\stackrel{{\mathbb{P}}}{\longrightarrow}\int _{0}^{t}f^{{\prime}}(Z_{s})dM_{s},$

ponadto z twierdzenia Lebesgue'a dla zwykłej całki,

$\int _{0}^{t}f^{{\prime}}(Z_{s}^{{(n)}})dA_{s}\rightarrow\int _{0}^{t}f^{{\prime}}(Z_{s})dA_{s}\quad\mbox{p.n..}$

Podobnie $\sup _{n}\sup _{{s\leq t}}|f^{{\prime\prime}}(Z_{s}^{{(n)}})|<\infty$ p.n. i ponownie stosując twierdzenie Lebesgue'a dostajemy

$\int _{0}^{t}f^{{\prime\prime}}(Z_{s}^{{(n)}})d\langle M\rangle _{s}\rightarrow\int _{0}^{t}f^{{\prime\prime}}(Z_{s})d\langle M\rangle _{s}\quad\mbox{p.n..}$

Oczywiście $f(Z_{t}^{{(n)}})\rightarrow f(Z_{t})$ p.n., więc możemy przejść w (13.2) z $n$ do $\infty$ , by dostać (13.1).

∎

Wniosek 13.1

Dla $f\in C^{2}({\mathbb{R}})$ ,

$f(W_{t})=f(0)+\int _{0}^{t}f^{{\prime}}(W_{s})dW_{s}+\frac{1}{2}\int _{0}^{t}f^{{\prime\prime}}(W_{s})ds.$

W podobny sposób jak w przypadku jednowymiarowym możemy udowodnić wielowymiarową wersję twierdzenia Itô.

Twierdzenie 13.2

Załóżmy, że $f\colon{\mathbb{R}}^{d}\rightarrow{\mathbb{R}}$ jest funkcją klasy $C^{2}$ oraz $Z=(Z^{{(1)}},\ldots,Z^{{(d)}})$ , gdzie $Z^{{(i)}}=Z_{0}^{{(i)}}+M^{{(i)}}+A^{{(i)}}$ są ciągłymi semimartyngałami dla $i=1,\ldots,d$ . Wówczas $f(Z)$ jest semimartyngałem oraz

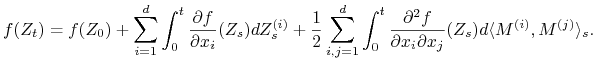$f(Z_{t})=f(Z_{0})+\sum _{{i=1}}^{d}\int _{0}^{t}\frac{\partial f}{\partial x_{i}}(Z_{s})dZ^{{(i)}}_{s}+\frac{1}{2}\sum _{{i,j=1}}^{d}\int _{0}^{t}\frac{\partial^{2}f}{\partial x_{i}\partial x_{j}}(Z_{s})d\langle M^{{(i)}},M^{{(j)}}\rangle _{s}.$

13.2. Twierdzenie Levy'ego

Twierdzenie 13.3 (Levy)

Załóżmy, że $M$ jest ciągłym martyngałem lokalnym takim, że $M_{0}=0$ oraz $M_{t}^{2}-t$ jest martyngałem lokalnym. Wówczas $M$ jest procesem Wienera.

Musimy wykazać, że dla $s<t$ , $M_{t}-M_{s}$ jest niezależne od ${\cal F}_{s}$ oraz ma rozkład ${\cal N}(0,t-s)$ . W tym celu wystarczy wykazać, że

${\mathbb{E}}(e^{{ih(M_{t}-M_{s})}}|{\mathcal{F}}_{s})=e^{{-\frac{1}{2}(t-s)h^{2}}}\quad\mbox{ dla }t>s\geq 0,\ h\in{\mathbb{R}}.$

(13.3)

Istotnie (13.3) implikuje, że ${\mathbb{E}}e^{{ih(M_{t}-M_{s})}}=\exp(-\frac{1}{2}(t-s)h^{2})$ dla $h\in{\mathbb{R}}$ , czyli $M_{t}-M_{s}\sim{\cal N}(0,t-s)$ . Ponadto dla dowolnej ${\mathcal{F}}_{s}$ -mierzalnej zmiennej $\eta$ oraz $h_{1},h_{2}\in{\mathbb{R}}$ ,

	$\displaystyle{\mathbb{E}}e^{{ih_{1}(M_{t}-M_{s})+ih_{2}\eta}}$	$\displaystyle={\mathbb{E}}[e^{{ih_{2}\eta}}{\mathbb{E}}(e^{{ih_{1}(M_{t}-M_{s})}}\|{\mathcal{F}}_{s})]$
		$\displaystyle={\mathbb{E}}[e^{{ih_{2}\eta}}e^{{-\frac{1}{2}(t-s)h_{1}^{2}}}]={\mathbb{E}}e^{{ih_{2}\eta}}{\mathbb{E}}e^{{ih_{1}(M_{t}-M_{s})}}.$

Zatem $M_{t}-M_{s}$ jest niezależne od zmiennych ${\mathcal{F}}_{s}$ -mierzalnych, czyli jest niezależne od ${\mathcal{F}}_{s}$ .

Zastosujmy wzór Itô dla $f(x)=e^{{ihx}}$ (wzór Itô zachodzi też dla funkcji zespolonych, wystarczy dodać odpowiednie równości dla części rzeczywistej i urojonej),

	$\displaystyle e^{{ihM_{t}}}$	$\displaystyle=f(M_{t})=f(M_{0})+\int _{0}^{t}f^{{\prime}}(M_{u})dM_{u}+\frac{1}{2}\int _{0}^{t}f^{{\prime\prime}}(M_{u})d\langle M\rangle _{u}$
		$\displaystyle=1+ih\int _{0}^{t}e^{{ihM_{u}}}dM_{u}-\frac{h^{2}}{2}\int _{0}^{t}e^{{ihM_{u}}}du$
		$\displaystyle=e^{{ihM_{s}}}+ih\int _{s}^{t}e^{{ihM_{u}}}dM_{u}-\frac{h^{2}}{2}\int _{s}^{t}e^{{ihM_{u}}}du.$

Niech $N:=\int _{0}^{t}e^{{ihM}}dM$ , wówczas $N$ jest martyngałem lokalnym oraz z nierówności Dooba (Twierdzenie 9.3),

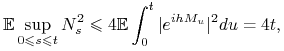${\mathbb{E}}\sup _{{0\leq s\leq t}}N_{s}^{2}\leq 4{\mathbb{E}}\int _{0}^{t}|e^{{ihM_{u}}}|^{2}du=4t,$

czyli $N$ jest na każdym przedziale skończonym majoryzowany przez zmienną całkowalną, zatem jest martyngałem. Ustalmy $A\in{\mathcal{F}}_{s}$ , wtedy

	$\displaystyle{\mathbb{E}}[e^{{ihM_{t}}}{\mathrm{I}}_{A}]$	$\displaystyle={\mathbb{E}}[e^{{ihM_{s}}}{\mathrm{I}}_{A}]+{\mathbb{E}}[(N_{t}-N_{s}){\mathrm{I}}_{A}]-\frac{h^{2}}{2}{\mathbb{E}}\Big[\int _{s}^{t}e^{{ihM_{u}}}du{\mathrm{I}}_{A}\Big]$
		$\displaystyle={\mathbb{E}}[e^{{ihM_{s}}}{\mathrm{I}}_{A}]-\frac{h^{2}}{2}\int _{s}^{t}{\mathbb{E}}[e^{{ihM_{u}}}{\mathrm{I}}_{A}]du.$

Zdefiniujmy $g(u)={\mathbb{E}}[e^{{ihM_{{s+u}}}}{\mathrm{I}}_{A}]$ , wtedy

$g(t-s)=g(0)-\frac{h^{2}}{2}\int _{s}^{t}g(u-s)du,$

czyli

$g(r)=g(0)-\frac{h^{2}}{2}\int _{0}^{r}g(u)du.$

Funkcja $g$ jest ciągła, a zatem z powyższego wzoru jest różniczkowalna i spełnia równanie różniczkowe

$g^{{\prime}}(r)=-\frac{h^{2}}{2}g(r).$

Zatem $g(r)=g(0)\exp(-\frac{1}{2}h^{2}r)$ dla $r\geq 0$ , czyli

${\mathbb{E}}[e^{{ihM_{t}}}{\mathrm{I}}_{A}]={\mathbb{E}}[e^{{ihM_{s}}}{\mathrm{I}}_{A}]e^{{-\frac{1}{2}h^{2}(t-s)}}={\mathbb{E}}[e^{{ihM_{s}-\frac{1}{2}h^{2}(t-s)}}{\mathrm{I}}_{A}],$

stąd ${\mathbb{E}}(e^{{ihM_{t}}}|{\mathcal{F}}_{s})=\exp(ihM_{s}-\frac{1}{2}h^{2}(t-s))$ p.n. i

${\mathbb{E}}(e^{{ih(M_{t}-M_{s})}}|{\mathcal{F}}_{s})=e^{{-ihM_{s}}}{\mathbb{E}}(e^{{ihM_{t}}}|{\mathcal{F}}_{s})=e^{{-\frac{1}{2}h^{2}(t-s)}}.$

∎

Uwaga 13.1

Równoważnie Twierdzenie Levy'go można sformułować w następujący sposób:
Jeśli $M\in{\mathcal{M}}^{c}_{{{\rm loc}}}$ oraz $\langle M\rangle=t$ , to $M-M_{0}$ jest procesem Wienera.

Uwaga 13.2

Założenie ciągłości $M$ jest fundamentalne. Jeśli położymy $M_{t}=N_{t}-t$ , gdzie $N$ jest procesem Poissona z parametrem 1, to $M_{t}^{2}-t$ jest martyngałem, a oczywiście $M$ nie jest procesem Wienera.

Można też udowodnić wielowymiarową wersję twierdzenia Levy'ego.

Twierdzenie 13.4

Załóżmy, że $M^{{(1)}},\ldots,M^{{(d)}}$ są ciągłymi martyngałami lokalnymi takimi, że $M^{{(i)}}_{0}=0$ oraz $M^{{(i)}}_{t}M^{{(j)}}_{t}-\delta _{{i,j}}t$ są martyngałami lokalnymi dla $1\leq i,j\leq d$ . Wówczas $M=(M^{{(1)}},\ldots,M^{{(d)}})$ jest $d$ -wymiarowym procesem Wienera.

13.3. Charakteryzacja procesu Wienera za pomocą martyngałów wykładniczych

Twierdzenie 13.5

Załóżmy, że proces $M$ jest ciągły, adaptowalny oraz $M_{0}=0$ . Wówczas $M$ jest procesem Wienera wtedy i tylko wtedy, gdy dla wszystkich $\lambda\in{\mathbb{R}}$ , $\exp(\lambda M_{t}-\lambda^{2}t/2)$ jest martyngałem lokalnym.

To, że $\exp(\lambda W_{t}-\lambda^{2}t/2)$ jest martyngałem jest prostym i dobrze znanym faktem. Wystarczy więc udowodnić implikację ” $\Leftarrow$ ”.

Określmy $\tau _{n}:=\inf\{ t>0\colon|M_{t}|\geq n\}\wedge n$ , wówczas $\tau _{n}\nearrow\infty$ oraz dla wszystkich $\lambda$ proces $X_{t}(\lambda)=\exp(\lambda M_{{t\wedge\tau _{n}}}-\lambda^{2}t\wedge\tau _{n}/2)$ jest ograniczonym martyngałem lokalnym (z dołu przez $0$ , z góry przez $e^{{|\lambda|n}}$ ), a więc martyngałem. Stąd

${\mathbb{E}}[X_{{t}}(\lambda){\mathrm{I}}_{A}]={\mathbb{E}}[X_{s}(\lambda){\mathrm{I}}_{A}]\quad\mbox{ dla }s<t,\ A\in{\mathcal{F}}_{s}.$

Zauważmy, że $X_{t}(0)=1$ oraz

$\Big|\frac{dX_{t}(\lambda)}{d\lambda}\Big|=|X_{t}(\lambda)(M_{{t\wedge\tau _{n}}}-\lambda t\wedge\tau _{n})|\leq e^{{\lambda _{0}n}}(n+\lambda _{0}n)\quad\mbox{ dla }|\lambda|\leq\lambda _{0}.$

Stąd, z Twierdzenia Lebesque'a o zbieżności zmajoryzowanej dla $t<s$ , $A\in{\mathcal{F}}_{s}$ ,

	$\displaystyle{\mathbb{E}}$	$\displaystyle[X_{t}(\lambda)(M_{{t\wedge\tau _{n}}}-\lambda t\wedge\tau _{n}){\mathrm{I}}_{A}]=\lim _{{h\rightarrow 0}}{\mathbb{E}}\Big[\frac{1}{h}(X_{t}(\lambda+h)-X_{t}(\lambda)){\mathrm{I}}_{A}\Big]$
		$\displaystyle=\lim _{{h\rightarrow 0}}{\mathbb{E}}\Big[\frac{1}{h}(X_{s}(\lambda+h)-X_{s}(\lambda)){\mathrm{I}}_{A}\Big]={\mathbb{E}}[X_{s}(\lambda)(M_{{s\wedge\tau _{n}}}-\lambda s\wedge\tau _{n}){\mathrm{I}}_{A}].$

Biorąc $\lambda=0$ dostajemy ${\mathbb{E}}[M_{{t\wedge\tau _{n}}}{\mathrm{I}}_{A}]={\mathbb{E}}[M_{{s\wedge\tau _{n}}}{\mathrm{I}}_{A}]$ , czyli $M^{{\tau _{n}}}$ jest martyngałem, a więc $M\in{\mathcal{M}}^{{2,c}}_{{{\rm loc}}}$ .

By skorzystać z twierdzenia Levy'ego i zakończyć dowód musimy jeszcze wykazać, że $M_{t}^{2}-t\in{\mathcal{M}}^{{2,c}}_{{{\rm loc}}}$ . Szacujemy dla $|\lambda|\leq\lambda _{0}$ ,

$\Big|\frac{d^{2}X_{t}(\lambda)}{d\lambda^{2}}\Big|=|X_{t}(\lambda)[(M_{{t\wedge\tau _{n}}}-t\wedge\tau _{n})^{2}-t\wedge\tau _{n}]|\leq e^{{\lambda _{0}n}}[(n+\lambda _{0}n)^{2}+n],$

skąd w podobny sposób jak dla pierwszych pochodnych dowodzimy, że dla $t<s$ , $A\in{\mathcal{F}}_{s}$ ,

${\mathbb{E}}[X_{t}(\lambda)((M_{{t\wedge\tau _{n}}}-\lambda t\wedge\tau _{n})^{2}-t\wedge\tau _{n}){\mathrm{I}}_{A}]={\mathbb{E}}[X_{s}(\lambda)((M_{{s\wedge\tau _{n}}}-\lambda s\wedge\tau _{n})^{2}-s\wedge\tau _{n}){\mathrm{I}}_{A}].$

Podstawiając $\lambda=0$ dostajemy

${\mathbb{E}}[(M_{{t\wedge\tau _{n}}}^{2}-t\wedge\tau _{n}){\mathrm{I}}_{A}]={\mathbb{E}}[(M_{{s\wedge\tau _{n}}}^{2}-s\wedge\tau _{n}){\mathrm{I}}_{A}],$

czyli $(M^{2}_{t}-t)^{{\tau _{n}}}$ jest martyngałem, więc $M_{t}^{2}-t\in{\mathcal{M}}^{{2,c}}_{{{\rm loc}}}$ .

∎

13.4. Zadania

Ćwiczenie 13.1

Korzystając ze wzoru Itô oblicz $\langle W_{t}^{2}\rangle$ oraz $\langle W_{t},e^{{W_{t}}}\rangle$ .

Ćwiczenie 13.2

Niech $Z_{{t}}=\exp(\lambda W_{{t}}-\lambda^{{2}}t/2)$ . Wykaż, że $dZ_{{t}}=\lambda Z_{{t}}dW_{{t}}$ tzn. $Z_{{t}}=1+\lambda\int _{{0}}^{{t}}Z_{{s}}dW_{{s}}$ .

Ćwiczenie 13.3

Niech $f$ będzie funkcją klasy $C^{{2}}$ na ${\mathbb{R}}^{{2}}$ , korzystając z wzoru Itô oblicz $df(t,W_{{t}})$ .

Ćwiczenie 13.4

Niech $M$ będzie ciągłym martyngałem lokalnym. Wykaż, że proces $N_{t}=\exp(M_{t}-\frac{1}{2}\langle M\rangle _{t})$ jest ciągłym martyngałem lokalnym oraz nadmartyngałem. Ponadto jeśli $M$ jest ograniczony, to $N$ jest martyngałem.

Ćwiczenie 13.5

Niech $g\colon{\mathbb{R}}^{{d}}\rightarrow{\mathbb{R}}$ będzie funkcją klasy $C^{{2}}$ , $G$ zbiorem otwartym ograniczonym w ${\mathbb{R}}^{{d}}$ oraz $x\in G$ . Określmy $\tau:=\inf\{ t\colon W_{{t}}+x\notin G\}$ . Korzystając ze wzoru Itô wykaż, że jeśli $g$ jest harmoniczna w $G$ , to $h(W_{{t}}^{{\tau}}+x)$ jest martyngałem. Pokaż, że wystarczy zakładać, iż $g$ jest klasy $C^{{2}}$ w pewnym otoczeniu domknięcia $G$ .

Ćwiczenie 13.6

Wykaż, że dla 3-wymiarowego ruchu Browna $W_{{t}}$ i $a\in{\mathbb{R}}^{{3}},a\neq 0$ proces $X_{{t}}=|W_{{t}}-a|^{{-1}}$ jest martyngałem lokalnym, ale nie jest martyngałem. Ponadto $X_{{t}}$ jest nadmartyngałem oraz zbiega do 0 w $L_{1}$ i prawie na pewno.

Ćwiczenie 13.7

Wykaż, że 2-wymiarowego ruchu Browna $W_{{t}}$ i $a\in{\mathbb{R}}^{{2}},a\neq 0$ proces $X_{{t}}=\ln|W_{{t}}-a|$ jest martyngałem lokalnym. Wywnioskuj stąd, że z prawdopodobieństwem 1 proces $W_{{t}}$ omija punkt $a$ , ale trajektoria procesu jest dowolnie bliska punktu $a$ .

Ćwiczenie 13.8

Załóżmy, że $W=(W^{{(1)}},W^{{(2)}},W^{{(3)}})$ jest trójwymiarowym procesem Wienera oraz

$X_{t}:=\int _{0}^{t}\sin(W_{t}^{{(3)}})dW_{t}^{{(1)}}+\int _{0}^{t}\cos(W_{t}^{{(3)}})dW_{t}^{{(2)}}.$

Wykaż, że $X$ jest procesem Wienera.

Ćwiczenie 13.9

Udowodnij Twierdzenie 13.4.

Ćwiczenie 13.10

Niech $T<\infty$ oraz $X=(X_{{t}})_{{0\leq t<T}}$ będzie procesem prognozowalnym takim, że dla pewnej liczby całkowitej $m\geq 1$ zachodzi

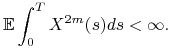${\mathbb{E}}\int _{{0}}^{{T}}X^{{2m}}(s)ds<\infty.$

Wykaż, że $X\in{\mathcal{L}}^{{2}}_{{T}}$ oraz $M=\int XdW$ jest martyngałem takim, że

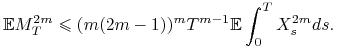${\mathbb{E}}M_{{T}}^{{2m}}\leq(m(2m-1))^{{m}}T^{{m-1}}{\mathbb{E}}\int _{{0}}^{{T}}X_{{s}}^{{2m}}ds.$

Wskazówka:

Zastosuj wzór Itô i nierówność Höldera.

Ćwiczenie 13.11

Niech $W=(W^{{1}},\ldots,W^{{d}})$ będzie $d$ -wymiarowym ruchem Browna, a $R_{{t}}=\| W_{{t}}\|$ . Wykaż, że
a) $B_{{t}}:=\sum _{{j=1}}^{{d}}\int _{{0}}^{{t}}\frac{W_{{s}}^{{(i)}}}{R_{{s}}}dW_{{s}}^{{i}}$ jest jednowymiarowym procesem Wienera;
b) $R_{{t}}=\int _{{0}}^{{t}}\frac{d-1}{2R_{{s}}}ds+B_{{t}}$ ( $R_{{t}}$ jest nazywane procesem Bessela).

Ćwiczenie 13.12

Niech $Z=Z_{{0}}+A+M,Y=Y_{{0}}+B+N$ będą ciągłymi semimartyngałami. Definiujemy całkę Stratonowicza wzorem

$\int _{{0}}^{{t}}Y_{{s}}\circ dZ_{{s}}:=\int _{{0}}^{{t}}Y_{{s}}dZ_{{s}}+\frac{1}{2}\langle M,N\rangle.$

Pokazać, że jeśli $f$ jest funkcją klasy $C^{{3}}$ na ${\mathbb{R}}$ , to

$f(Z_{{t}})=f(Z_{{0}})+\int _{{0}}^{{t}}f^{{\prime}}(Z_{{s}})\circ dZ_{{s}}.$

Ćwiczenie 13.13

Pokazać, że przy oznaczeniach poprzedniego zadania oraz dowolnym ciągu $\pi _{{n}}=\{ t_{{0}}^{{(n)}},t_{{1}}^{{(n)}},\ldots,t_{{k_{n}}}^{{(n)}}\}$ podziałów odcinka $[0,t]$ takim, że $\mathrm{diam}(\pi _{{n}})\rightarrow 0$ zachodzi

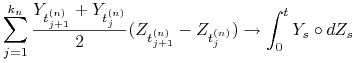$\sum _{{j=1}}^{{k_{{n}}}}\frac{Y_{{t_{{j+1}}^{{(n)}}}}+Y_{{t_{{j}}^{{(n)}}}}}{2}(Z_{{t_{{j+1}}^{{(n)}}}}-Z_{{t_{{j}}^{{(n)}}}})\rightarrow\int _{{0}}^{{t}}Y_{{s}}\circ dZ_{{s}}$

przy $n\rightarrow\infty$ według prawdopodobieństwa.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.