Zagadnienia

2.1 $\sigma$ -ciało zbiorów cylindrycznych
2.2 Warunki zgodności. Twierdzenie Kołmogorowa o istnieniu procesu
2.3 Uwagi i uzupełnienia
2.4 Zadania

2. Rozkłady procesów stochastycznych

Podczas tego wykładu zdefiniujemy rozkład procesu stochastycznego, w szczególności powiemy jakie zdarzenia określone przez proces są mierzalne. Udowodnimy, że rozkład procesu jest wyznaczony przez rozkłady skończenie wymiarowe. Sformułujemy też warunki, które muszą być spełnione, by istniał proces stochastyczny o zadanych rozkładach skończenie wymiarowych.

Przypomnijmy, że jeśli $X$ jest zmienną losową o wartościach w przestrzeni mierzalnej $(E,{\mathcal{E}})$ , to rozkładem $X$ jest miara probabilistyczna na $(E,{\mathcal{E}})$ zadana wzorem

$\mu _{{X}}(A)={\mathbb{P}}(X\in A),\ A\in{\mathcal{E}}.$

Dla uproszczenia będziemy przyjmować, że proces $X$ przyjmuje wartości rzeczywiste.

2.1. 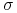$\sigma$ -ciało zbiorów cylindrycznych

Proces $X=(X_{{t}})_{{t\in T}}$ możemy traktować jako zmienną losową o wartościach w ${\mathbb{R}}^{{T}}$ . Jakie podzbiory ${\mathbb{R}}^{{T}}$ są wówczas na pewno mierzalne?

Definicja 2.1

Zbiory postaci

$\big\{ x\in{\mathbb{R}}^{{T}}\colon(x_{{t_{{1}}}},\ldots,x_{{t_{{n}}}})\in A\big\},\quad t_{{1}},\ldots,t_{{n}}\in T,A\in{\mathcal{B}}({\mathbb{R}}^{{n}})$

nazywamy zbiorami cylindrycznymi. Przez ${\mathcal{B}}({\mathbb{R}}^{{T}})$ będziemy oznaczać najmniejsze $\sigma$ -ciało zawierające zbiory cylindryczne i będziemy je nazywać $\sigma$ -ciałem zbiorów cylindrycznych.

Uwaga 2.1

Zauważmy, że

${\mathcal{B}}({\mathbb{R}}^{{T}})=\sigma(\{ x\in{\mathbb{R}}^{{T}}\colon x_{{t}}\in A\},\ t\in T,A\in{\mathcal{B}}({\mathbb{R}})).$

Przykład 2.1

Zbiory $\{ x\colon x_{{t}}>x_{{s}}\}$ , $\{ x\colon x_{{t_{{1}}}}>0,x_{{t_{{2}}}}-x_{{t_{{1}}}}>0,\ldots,x_{{t_{{n}}}}-x_{{t_{{n-1}}}}>0\}$ oraz $\{ x\colon\forall _{{t<s,t,s\in{\mathbb{Q}}_{{+}}}}\ x_{{t}}>x_{{s}}\}$ należą do ${\mathcal{B}}({\mathbb{R}}^{{[0,\infty)}})$ .

Przykład 2.2

Zbiór $\{ x\colon\sup _{{t\in T}}|x_{{t}}|\leq 1\}$ nie należy do ${\mathcal{B}}({\mathbb{R}}^{{T}})$ , gdy $T$ jest nieprzeliczalny, podobnie $\{ x\colon t\rightarrow x_{{t}}\mbox{ ciągłe}\}$ nie należy do ${\mathcal{B}}({\mathbb{R}}^{{T}})$ , gdy $T$ jest niezdegenerowanym przedziałem.

Definicja 2.2

Rozkładem procesu $X=(X_{{t}})_{{t\in T}}$ nazywamy miarę probabilistyczną $\mu _{{X}}$ na ${\mathcal{B}}({\mathbb{R}}^{{T}})$ daną wzorem

$\mu _{{X}}(C)={\mathbb{P}}((X_{{t}})_{{t\in T}}\in C),\ C\in{\mathcal{B}}({\mathbb{R}}^{{T}}).$

Uwaga 2.2

Załóżmy, że $T$ jest przedziałem (skończonym lub nie). Na przestrzeni funkcji ciagłych $C(T)$ rozważmy topologię zbieżności niemal jednostajnej. Wówczas ${\mathcal{B}}({\mathbb{R}}^{{T}})\cap C(T)={\mathcal{B}}(C(T))$ , co oznacza, że jeśli proces $X=(X_{{t}})_{{t\in T}}$ ma ciągłe trajektorie, to $X$ wyznacza rozkład probabilistyczny na przestrzeni funkcji ciągłych $(C(T),{\mathcal{B}}(C(T)))$ . W szczególności proces Wienera wyznacza pewien rozkład probabilistyczny na $C[0,\infty)$ .

2.2. Warunki zgodności. Twierdzenie Kołmogorowa o istnieniu procesu

Najprostsze zbiory z ${\mathcal{B}}({\mathbb{R}}^{{T}})$ to zbiory cylindryczne. Miary takich zbiorów to rozkłady skończenie wymiarowe procesu.

Definicja 2.3

Dla procesu $(X_{{t}})_{{t\in T}}$ o wartościach w ${\mathbb{R}}$ i $t_{{1}},\ldots,t_{{n}}\in T$ określamy miarę $\mu _{{t_{{1}},\ldots,t_{{n}}}}$ na ${\mathbb{R}}^{{n}}$ wzorem

$\mu _{{t_{{1}},\ldots,t_{{n}}}}(A)={\mathbb{P}}((X_{{t_{{1}}}},\ldots,X_{{t_{{n}}}})\in A),\quad A\in{\mathcal{B}}({\mathbb{R}}^{{n}}).$

Rodzinę miar $\{\mu _{{t_{{1}},\ldots,t_{{n}}}}\colon t_{{1}},\ldots,t_{{n}}\in T\mbox{ parami różne}\}$ nazywamy rodziną skończenie wymiarowych rozkładów procesu $X$ .

Stwierdzenie 2.1

Załóżmy, że $X=(X_{{t}})_{{t\in T}}$ i $Y=(Y_{{t}})_{{t\in T}}$ są procesami o tych samych skończenie wymiarowych rozkładach, czyli

${\mathbb{P}}((X_{{t_{{1}}}},\ldots,X_{{t_{{n}}}})\in A)={\mathbb{P}}((Y_{{t_{{1}}}},\ldots,Y_{{t_{{n}}}})\in A)$

dla wszystkich $t_{{1}},\ldots,t_{{n}}\in T,A\in{\mathcal{B}}({\mathbb{R}}^{{n}})$ . Wówczas $X$ i $Y$ mają ten sam rozkład, tzn.

${\mathbb{P}}(X\in C)={\mathbb{P}}(Y\in C)\mbox{ dla wszystkich }C\in{\mathcal{B}}({\mathbb{R}}^{T}).$

Rodzina zbiorów cylindrycznych ${\mathcal{A}}$ tworzy $\pi$ -układ, a rodzina ${\cal C}$ zbiorów $C$ takich, że ${\mathbb{P}}(X\in C)={\mathbb{P}}(Y\in C)$ , jest $\lambda$ -układem zawierającym ${\mathcal{A}}$ . Zatem z twierdzenia o $\pi$ - i $\lambda$ - układach, ${\cal C}$ zawiera również $\sigma$ -ciało generowane przez ${\mathcal{A}}$ , czyli ${\mathcal{B}}({\mathbb{R}}^{{T}})$ .

∎

Definicja 2.4

Powiemy, że rodzina skończenie wymiarowych rozkładów

$\{\mu _{{t_{{1}},\ldots,t_{{n}}}}\colon\ t_{{1}},\ldots,t_{{n}}\in T\mbox{ parami różne}\}$

spełnia warunki zgodności, jeśli zachodzą następujące warunki:

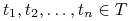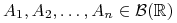i) Dla dowolnych $t_{{1}},t_{{2}},\ldots,t_{{n}}\in T$ , dowolnej permutacji $(i_{{1}},\ldots,i_{{n}})$ liczb $(1,\ldots,n)$ oraz zbiorów $A_{1},A_{2},\ldots,A_{n}\in{\mathcal{B}}({\mathbb{R}})$ ,

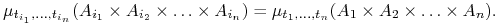
$\mu _{{t_{{i_{{1}}}},\ldots,t_{{i_{{n}}}}}}(A_{{i_{{1}}}}\times A_{{i_{{2}}}}\times\ldots\times A_{{i_{{n}}}})=\mu _{{t_{{1}},\ldots,t_{{n}}}}(A_{{1}}\times A_{{2}}\times\ldots\times A_{{n}}).$
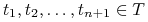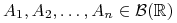ii) Dla dowolnych $t_{{1}},t_{{2}},\ldots,t_{{n+1}}\in T$ oraz $A_{1},A_{2},\ldots,A_{n}\in{\mathcal{B}}({\mathbb{R}})$ ,

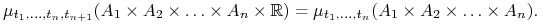
$\mu _{{t_{{1}},\ldots,t_{{n}},t_{{n+1}}}}(A_{{1}}\times A_{{2}}\times\ldots\times A_{{n}}\times{\mathbb{R}})=\mu _{{t_{{1}},\ldots,t_{{n}}}}(A_{{1}}\times A_{{2}}\times\ldots\times A_{{n}}).$

Oczywiście rodzina rozkładów skończenie wymiarowych dowolnego procesu stochastycznego spełnia warunki zgodności. Okazuje się, że są to jedyne warunki jakie należy nałożyć na taką rodzinę.

Twierdzenie 2.1

Załóżmy, że dana jest rodzina skończenie wymiarowych rozkładów $(\mu _{{t_{{1}},\ldots,t_{{n}}}})$ spełniająca warunki zgodności. Wówczas istnieje proces $(X_{{t}})_{{t\in T}}$ mający skończenie wymiarowe rozkłady równe $(\mu _{{t_{{1}},\ldots,t_{{n}}}})$ .

Nie będziemy przedstawiać technicznego dowodu powyższego twierdzenia - wszystkich zainteresowanych odsyłamy do [8] lub [4]. W zamian sformułujemy użyteczny wniosek.

Wniosek 2.1

Załóżmy, że $T\subset{\mathbb{R}}$ oraz dana jest rodzina rozkładów skończenie wymiarowych $\{\mu _{{t_{{1}},\ldots,t_{{n}}}}\colon t_{1}<t_{2}<\ldots<t_{n},t_{1},\ldots,t_{n}\in T\}$ spełniająca warunek

	$\displaystyle\mu _{{t_{{1}},\ldots,t_{{n}}}}(A_{{1}}\times\ldots$	$\displaystyle\times A_{{k-1}}\times{\mathbb{R}}\times A_{{k+1}}\ldots\times A_{{n}})$
		$\displaystyle=\mu _{{t_{{1}},\ldots t_{{k-1}},t_{{k+1}},\ldots,t_{{n}}}}(A_{{1}}\times\ldots\times A_{{k-1}}\times A_{{k+1}}\times\ldots\times A_{{n}}).$

dla wszystkich $t_{1}<t_{2}<\ldots<t_{n}$ , $n\geq 2$ , $1\leq k\leq n$ oraz zbiorów borelowskich $A_{1},\ldots,A_{n}$ . Wówczas istnieje proces $(X_{t})_{{t\in T}}$ taki, że $(X_{{t_{1}}},\ldots,X_{{t_{n}}})$ ma rozkład $\mu _{{t_{{1}},\ldots,t_{{n}}}}$ dla $t_{1}<t_{2}<\ldots<t_{n}$ .

Dla $t_{1},\ldots,t_{n}\in T$ parami różnych istnieje permutacja $(i_{1},\ldots,i_{n})$ liczb $(1,\ldots,n)$ taka, że $t_{{i_{1}}}<t_{{i_{2}}}<\ldots<t_{{i_{n}}}$ . Możemy więc określić $\mu _{{t_{1},\ldots,t_{n}}}$ jako rozkład wektora $(Y_{1},\ldots,Y_{n})$ takiego, że $(Y_{{i_{1}}},\ldots,Y_{{i_{n}}})$ ma rozkład $\mu _{{t_{{i_{1}}},\ldots,t_{{i_{n}}}}}$ . Nietrudno sprawdzić, że tak określona rodzina miar $(\mu _{{t_{1},\ldots,t_{n}}})$ spełnia warunki zgodności.

∎

Przykład 2.3

Jeśli $(\mu _{{t}})_{{t\in T}}$ jest dowolną rodziną rozkładów na ${\mathbb{R}}$ , to istnieje rodzina niezależnych zmiennych losowych $(X_{{t}})_{{t\in T}}$ taka, że $X_{{t}}$ ma rozkład $\mu _{{t}}$ . Używamy tu twierdzenia o istnieniu dla $\mu _{{t_{{1}},\ldots,t_{{n}}}}=\mu _{{t_{{1}}}}\otimes\ldots\otimes\mu _{{t_{{n}}}}$ .

Przykład 2.4

Istnieje proces spełniający warunki (W0)-(W2) definicji procesu Wienera. Istotnie dla $0=t_{{0}}\leq t_{{1}}<t_{{2}}<\ldots<t_{{n}}$ kładziemy

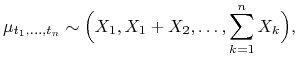$\mu _{{t_{{1}},\ldots,t_{{n}}}}\sim\Big(X_{{1}},X_{{1}}+X_{{2}},\ldots,\sum _{{k=1}}^{{n}}X_{{k}}\Big),$

gdzie $X_{{1}},\ldots,X_{{n}}$ są niezależnymi zmiennymi losowymi $X_{{k}}\sim{\mathcal{N}}(0,t_{{k}}-t_{{k-1}})$ . Warunki zgodności wynikają wówczas stąd, iż jeśli $Y_{{1}},Y_{{2}}$ są niezależne i $Y_{{i}}\sim{\mathcal{N}}(0,\sigma _{{i}}^{{2}})$ dla $i=1,2$ , to $Y_{{1}}+Y_{{2}}\sim{\mathcal{N}}(0,\sigma _{{1}}^{{2}}+\sigma _{{2}}^{{2}})$ .

2.3. Uwagi i uzupełnienia

Podczas wykładu zakładaliśmy, że proces $X$ ma wartości rzeczywiste. Nic się zmieni (poza oczywistymi drobnymi zmianami definicji) dla procesów o wartościach w ${\mathbb{R}}^{{d}}$ . Czasem jednak zachodzi potrzeba rozpatrywania procesów o wartościach w ogólniejszej przestrzeni $E$ . Warto więc zauważyć, że

w Stwierdzeniu 2.1 nie wykorzystywaliśmy żadnych własności przestrzeni $E$ ,
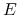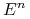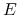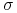w dowodzie Twierdzenia 2.1 wykorzystuje się regularność miar na $E^{n}$ – tu wystarczy założyć, że $E$ jest $\sigma$ -zwartą przestrzenią metryczną, tzn. 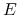$E$ jest przeliczalną sumą zbiorów zwartych lub dodać warunek regularności rozpatrywanych miar (definicje i podstawowe własności miar regularnych można znaleźć w rozdziale 2 [6]).

2.4. Zadania

Ćwiczenie 2.1

Udowodnij, że jeśli zbiór $A\in{\mathcal{B}}({\mathbb{R}}^{{T}})$ , to istnieje zbiór przeliczalny $T_{{0}}\subset T$ taki, że jeśli $x,y\in{\mathbb{R}}^{{T}}$ oraz $x(t)=y(t)$ dla $t\in T_{{0}}$ , to $x\in A\Leftrightarrow y\in A$ .

Ćwiczenie 2.2

Niech $T=[a,b]$ , $a<t_{{0}}<b$ , wykaż, że następujące zbiory nie należą do ${\mathcal{B}}({\mathbb{R}}^{{T}})$ :
i) $A_{{1}}=\{ x\in{\mathbb{R}}^{{T}}\colon\ \sup _{{t\in[a,b]}}|x_{{t}}|\leq 1\}$ ;
ii) $A_{{2}}=\{ x\in{\mathbb{R}}^{{T}}\colon\ t\rightarrow x_{{t}}\mbox{ ciągłe na }[a,b]\}$ ;
iii) $A_{{3}}=\{ x\in{\mathbb{R}}^{{T}}\colon\ \lim _{{t\rightarrow t_{{0}}}}x_{{t}}=0\}$ ;
iv) $A_{{4}}=\{ x\in{\mathbb{R}}^{{T}}\colon\ t\rightarrow x_{{t}}\mbox{ ciągłe w }t_{{0}}\}$ .
Wykaż mierzalność tych zbiorów przy założeniu ciągłości (prawostronnej ciągłości) trajektorii, tzn. wykaż, że wszystkie te zbiory po przecięciu z $C(T)$ (odp. $RC(T)$ –przestrzeni funkcji prawostronnie ciągłych) należą do ${\mathcal{B}}({\mathbb{R}}^{{T}})\cap C(T)$ ( ${\mathcal{B}}({\mathbb{R}}^{{T}})\cap RC(T)$ odp.).

Ćwiczenie 2.3

Niech $T=[a,b]$ . Wykaż, że ${\mathcal{F}}=\{ A\cap C(T)\colon A\in{\mathcal{B}}({\mathbb{R}}^{{T}})\}$ jest $\sigma$ -ciałem zbiorów borelowskich (w metryce supremum) na $C(T)$ .

Ćwiczenie 2.4

Wykaż, że istnieje proces $(X_{{t}})_{{t\geq 0}}$ o przyrostach niezależnych, startujący z 0 taki, że $X_{{t}}-X_{{s}}$ ma rozkład Cauchy'ego z parametrem $t-s$ (proces taki nazywamy procesem Cauchy'ego, bądź procesem 1-stabilnym).

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Analizy Stochastycznej