Zagadnienia

7.1 Całka Riemanna-Stieltjesa
7.2 Całka Lebesgue'a-Stieltjesa
7.3 Nieskończone wahanie ciągłych martyngałów
7.4 Zadania

7. Całka Stieltjesa

Podstawowy problem jakim się zajmiemy podczas najbliższych wykładów polega na ścisłym zdefiniowaniu całek $\int _{0}^{t}f(s)dW_{s}$ , $\int _{0}^{t}X_{s}dW_{s}$ lub ogólniej $\int _{0}^{t}X_{s}dY_{s}$ , gdzie $f(s)$ jest ,,porządną” funkcją, a $X_{s}$ , $Y_{s}$ są ,,porządnymi” procesami stochastycznymi.

Najprostsze podejście polega na zdefiniowaniu osobno całki dla każdej trajektorii, tzn. określeniu dla ustalonego $\omega\in\Omega$ , $\int _{0}^{s}Y_{s}(\omega)dX_{s}(\omega)$ . Sposób takiej konstrukcji daje całka Stieltjesa, uogólniająca całkę Riemanna.

7.1. Całka Riemanna-Stieltjesa

W tej części podamy tylko podstawowe fakty i definicje, bez dowodów. Więcej informacji oraz kompletne dowody można znaleźć w [2, 9] i [7].

Definicja 7.1

Podziałem przedziału $[a,b]$ nazywamy niemalejący ciąg liczb $\Pi=(t_{0},t_{1},\ldots,t_{k})$ taki, że $a=t_{0}\leq t_{1}\leq\ldots\leq t_{k}=b$ . Średnicę podziału $\Pi$ definiujemy wzorem $\mathrm{diam}(\Pi)\colon=\max _{{i}}|t_{{i+1}}-t_{{i}}|$ .
Mówimy, że podział $\Pi^{{\prime}}$ jest podpodziałem $\Pi$ (ozn. $\Pi^{{\prime}}\prec\Pi$ ) jeśli wszystkie punkty $\Pi$ są punktami $\Pi^{{\prime}}$ .
Ciąg $\Pi^{n}=(t_{0}^{n},\ldots,t_{{k_{n}}}^{n})$ nazywamy normalnym ciągiem podziałów, jeśli $\mathrm{diam}(\Pi^{n})\stackrel{n\rightarrow\infty}{\longrightarrow}0$ oraz $\Pi^{{n+1}}\prec\Pi^{n}$ .

Definicja 7.2

Niech $f,g\colon[a,b]\rightarrow{\mathbb{R}}$ . Powiemy że $\int _{a}^{b}g\, df$ istnieje oraz, że $g$ jest całkowalna względem $f$ , jeśli dla dowolnego normalnego ciągu podziałów $\Pi^{n}=(t_{0}^{n},\ldots,t_{{k_{n}}}^{n})$ oraz punktów $s_{0}^{n},\ldots,s_{{k_{n}-1}}^{n}$ takich, że $t_{j}^{k}\leq s_{j}^{k}\leq t_{{j+1}}^{k}$ istnieje skończona granica

$\lim _{{n\rightarrow\infty}}\sum _{{j=1}}^{{k_{n}}}g(s_{{j-1}}^{k})[f(t_{j}^{k})-f(t_{{j-1}}^{k})],$

która nie zależy od wybranego ciągu punktów i podziałów. Granicę tą oznaczamy $\int _{{a}}^{{b}}g(t)\, df(t)$ i nazywamy całką Riemanna-Stjeltjesa.

Uwaga 7.1

Można udowodnić, że całka $\int _{a}^{b}g\, df$ istnieje oraz jest równa $S$ , jeśli dla dowolnego $\varepsilon>0$ istnieje $\delta>0$ taka, że dla dowolnego podziału $\Pi^{n}=(t_{0}^{n},\ldots,t_{{k_{n}}}^{n})$ o średnicy nie większej niż $\delta$ oraz punktów $s_{0}^{n},\ldots,s_{{k_{n}-1}}^{n}$ takich, że $t_{j}^{k}\leq s_{j}^{k}\leq t_{{j+1}}^{k}$ ,

$\Big|S-\sum _{{j=1}}^{{k_{n}}}g(s_{{j-1}}^{k})[f(t_{j}^{k})-f(t_{{j-1}}^{k})]\Big|\leq\varepsilon.$

Uwaga 7.2

i) W przypadku $f(t)=t$ całka Riemanna-Stieltjesa jest całką Riemanna.
ii) Jeśli $f\in C^{1}[a,b]$ , to $f(t_{{j+1}}^{n})-f(t_{j}^{n})=f^{{\prime}}(\Theta _{j}^{n})$ dla pewnego $t_{j}^{{n+1}}\leq\Theta _{j}^{n}\leq t_{j}^{n}$ , stąd można prosto udowodnić, że w tym przypadku $\int _{{a}}^{{b}}g(t)\, df(t)=\int _{{a}}^{{b}}g(t)f^{{\prime}}(t)\, dt.$

Wprost z definicji natychmiast wynika.

Stwierdzenie 7.1

i) Jeśli $g_{1}$ i $g_{2}$ są całkowalne względem $f$ , to dla dowolnych liczb $c_{1}$ i $c_{2}$ funkcja $c_{1}g_{1}+c_{2}g_{2}$ jest całkowalna względem $f$ oraz

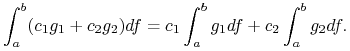$\int _{a}^{b}(c_{1}g_{1}+c_{2}g_{2})df=c_{1}\int _{a}^{b}g_{1}df+c_{2}\int _{a}^{b}g_{2}df.$

ii) Jeśli $g$ jest całkowalna względem $f_{1}$ i $f_{2}$ , to dla dowolnych liczb $c_{1}$ i $c_{2}$ , $g$ jest całkowalna względem $c_{1}f_{1}+c_{2}f_{2}$ oraz

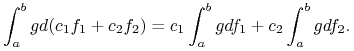$\int _{a}^{b}gd(c_{1}f_{1}+c_{2}f_{2})=c_{1}\int _{a}^{b}gdf_{1}+c_{2}\int _{a}^{b}gdf_{2}.$

Uwaga 7.3

Może się zdarzyć, że dla $a<b<c$ całki $\int _{a}^{b}gdf$ i $\int _{b}^{c}gdf$ istnieją, a całka $\int _{a}^{c}gdf$ nie istnieje. Jeśli jednak wszystkie trzy całki istnieją, to $\int _{a}^{c}gdf=\int _{a}^{b}gdf+\int _{b}^{c}gdf$ .

Oczywiście naturalnie jest zapytać dla jakich funkcji $f$ i $g$ istnieje całka $\int gdf$ . By odpowiedzieć na to pytanie musimy zdefiniować funkcje o wahaniu skończonym.

Definicja 7.3

Jeśli $f\colon[a,b]\rightarrow{\mathbb{R}}$ , to liczbę

$\mathrm{Wah}_{{[a,b]}}(f)\colon=\sup\limits _{{n\in\mathbb{N}}}\,\sup _{{a=t_{0}<\ldots<t_{n}=b}}\,\sum _{{i=1}}^{{n}}|f(t_{i})-f(t_{{i-1}})|$

nazywamy wahaniem funkcji $f$ w przedziale $[a,b]$ . Mówimy, że $f$ ma wahanie skończone na $[a,b]$ , jeśli $\mathrm{Wah}_{{[a,b]}}(f)<\infty$ .

Oczywiście $0\leq\mathrm{Wah}_{{[a,b]}}(f)\leq\infty$ Wahanie jest addytywną funkcją przedziału, tzn. $\mathrm{Wah}_{{[a,c]}}(f)=\mathrm{Wah}_{{[a,b]}}(f)+\mathrm{Wah}_{{[b,c]}}(f)$ dla $a<b<c$ .

Przykład 7.1

Funkcje lipschitzowskie, funkcje monotoniczne mają wahanie skończone na ograniczonych przedziałach. Kombinacja liniowa funkcji o wahaniu skończonym ma wahanie skończone.

Przykład 7.2

Funkcja $f(x)=x\sin(\frac{1}{x})$ oraz $f(0)=0$ jest ciągła, ale nie ma wahania skończonego na $[0,1]$ .

Twierdzenie 7.1

Jeżeli $f,g\colon[a,b]\rightarrow{\mathbb{R}}$ , przy czym $g$ jest ciągła, a $f$ ma wahanie skończone, to $\int _{{a}}^{{b}}g\, df$ istnieje.

Twierdzenie to można odwrócić.

Twierdzenie 7.2

Jeśli całka Riemanna-Stieltjesa $\int _{a}^{b}gdf$ istnieje dla dowolnej funkcji ciągłej $g$ , to funkcja $f$ ma wahanie skończone na $[a,b]$ .

7.2. Całka Lebesgue'a-Stieltjesa

Stwierdzenie 7.2

Jeśli $f$ ma wahanie skończone na $[a,b]$ , to istnieją funkcje niemalejące $f_{1},f_{2}$ takie, że $f_{1}(a)=f_{2}(a)=0$ oraz $f(t)=f(a)+f_{1}(t)-f_{2}(t)$ . Co więcej $f$ ma w każdym punkcie granice jednostrone. Ponadto jeśli $f$ jest ciągła (odp. prawostronnie ciągła), to $f_{1}$ i $f_{2}$ można wybrać ciągłe (odp. prawostronnie ciągłe).

Szkic dowodu

Określamy $f_{1}(t)=\frac{1}{2}(\mathrm{Wah}_{{[a,t]}}(f)+f(t)-f(a))$ oraz $f_{2}(t)=\frac{1}{2}(\mathrm{Wah}_{{[a,t]}}(f)-f(t)+f(a))$ .

∎

Definicja 7.4

Załóżmy, że $f$ jest prawostronnie ciągłą funkcją na $[a,b]$ o wahaniu skończonym. Niech $f_{1}$ i $f_{2}$ będą prawostronnie ciągłymi funkcjami niemalejącymi takimi, że $f_{1}(a)=f_{2}(a)=0$ oraz $f(t)=f(a)+f_{1}(t)-f_{2}(t)$ . Istnieją wtedy skończone miary borelowskie $\mu _{1}$ i $\mu _{2}$ na $[a,b]$ takie, że $\mu _{i}[a,t]=f_{i}(t)$ dla $i=1,2$ . Dla ograniczonych funkcji mierzalnych $g$ na $[a,b]$ określamy całkę Lebesgue'a-Stieltjesa $g$ względem $f$ wzorem

$\int _{{[a,b]}}gdf=\int gd\mu _{1}-\int gd\mu _{2}.$

Uwaga 7.4

Można wykazać, że dla funkcji ciągłych $g$ całki Riemanna-Stieltjesa i Lebesgue'a-Stieltjesa $g$ względem $f$ są sobie równe.

7.3. Nieskończone wahanie ciągłych martyngałów

Niestety proces Wienera ma z prawdopodobieństwem jeden nieskończone wahanie na każdym przedziale. Prawdziwy jest znacznie ogólniejszy fakt.

Twierdzenie 7.3

Załóżmy, że $(M_{t})_{{t\in[a,b]}}$ jest ciągłym martyngałem oraz

$A=\{\omega\colon M_{t}(\omega)\mbox{ ma wahanie skończone na [a,b]}\}.$

Wówczas $M_{t}$ ma z prawdopodobieństwem 1 trajektorie stałe na $A$ , tzn.

${\mathbb{P}}(\forall _{{t\in[a,b]}}\ M_{t}{\mathrm{I}}_{A}=M_{a}{\mathrm{I}}_{A})=1.$

Załóżmy najpierw, że istnieje stała $C<\infty$ taka, że dla wszystkich $\omega\in\Omega$ , $\mathrm{Wah}_{{[a,b]}}(M_{t}(\omega))\leq C$ oraz $\sup _{{t\in[a,b]}}|M_{t}(\omega)|\leq C$ . Ustalmy $0\leq u\leq b-a$ i rozpatrzmy zmienne losowe

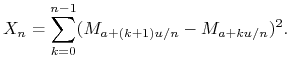$X_{n}=\sum _{{k=0}}^{{n-1}}(M_{{a+(k+1)u/n}}-M_{{a+ku/n}})^{2}.$

Dla $s<t$ mamy

${\mathbb{E}}M_{{s}}M_{{t}}={\mathbb{E}}{\mathbb{E}}(M_{{s}}M_{{t}}|{\mathcal{F}}_{s})={\mathbb{E}}(M_{s}{\mathbb{E}}(M_{t}|{\mathcal{F}}_{s}))={\mathbb{E}}M_{s}^{2},$

stąd

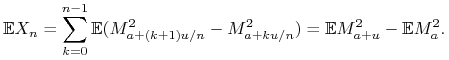${\mathbb{E}}X_{n}=\sum _{{k=0}}^{{n-1}}{\mathbb{E}}(M^{2}_{{a+(k+1)u/n}}-M^{2}_{{a+ku/n}})={\mathbb{E}}M^{2}_{{a+u}}-{\mathbb{E}}M^{2}_{a}.$

Szacujemy

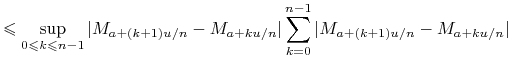	$\displaystyle\|X_{n}\|$	$\displaystyle\leq\sup _{{0\leq k\leq n-1}}\|M_{{a+(k+1)u/n}}-M_{{a+ku/n}}\|\sum _{{k=0}}^{{n-1}}\|M_{{a+(k+1)u/n}}-M_{{a+ku/n}}\|$
		$\displaystyle\leq\sup _{{\|s-t\|\leq u/n}}\|M_{t}-M_{s}\|\mathrm{Wah}_{{[a,b]}}(M_{t}),$

stąd $|X_{n}|\leq 2C^{2}$ oraz, z ciągłości $M$ , $\lim _{{n\rightarrow\infty}}X_{n}=0$ . Zatem z twierdzenia Lebesgue'a o zbieżności zmajoryzowanej $\lim _{{n\rightarrow\infty}}{\mathbb{E}}X_{n}=0$ , czyli ${\mathbb{E}}M^{2}_{{a+u}}={\mathbb{E}}M^{2}_{a}$ . Zauważmy jednak, że

	$\displaystyle{\mathbb{E}}M_{{a+u}}^{2}$	$\displaystyle={\mathbb{E}}{\mathbb{E}}((M_{a}+(M_{{a+u}}-M_{a}))^{2}\|{\mathcal{F}}_{a})$
		$\displaystyle={\mathbb{E}}M_{a}^{2}+{\mathbb{E}}(M_{{a+u}}-M_{a})^{2}+2{\mathbb{E}}[M_{a}{\mathbb{E}}((M_{{a+u}}-M_{a})\|{\mathcal{F}}_{a})$
		$\displaystyle={\mathbb{E}}M_{a}^{2}+{\mathbb{E}}(M_{{a+u}}-M_{a})^{2}.$

Stąd $M_{{a+u}}=M_{a}$ p.n., czyli $M_{t}=M_{a}$ p.n. dla dowolnego $t\in[a,b]$ . Z ciągłości $M$ wynika, że ${\mathbb{P}}(\forall _{{t}}\ M_{t}=M_{a})=1$ .

W przypadku ogólnym zdefiniujmy ciąg czasów zatrzymania

$\tau _{n}=\inf\{ t\geq a\colon\sup _{{a\leq s\leq t}}|M_{s}|\geq n\}\wedge\inf\{ t\geq a\colon\mathrm{Wah}_{{[0,t]}}\geq n\},$

wówczas martyngał $M^{{\tau _{n}}}$ spełnia założenia pierwszej części dowodu (z $C=n$ ), więc $M^{{\tau _{n}}}$ ma stałe trajektorie p.n.. Wystarczy zauważyć, że dla $\omega\in A$ , $\tau _{n}(\omega)=\infty$ dla dostatecznie dużych $n$ .

∎

7.4. Zadania

Ćwiczenie 7.1

Załóżmy, że $h$ jest niemalejącą funkcją ciągłą na przedziale $[a,b]$ . Udowodnij, że
a) Jeśli $g$ ma wahanie skończone, to $g\circ h$ też ma wahanie skończone.
b) Jeśli $\int _{{h(a)}}^{{h(b)}}fdg$ istnieje, to

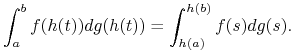$\int _{a}^{b}f(h(t))dg(h(t))=\int _{{h(a)}}^{{h(b)}}f(s)dg(s).$

Ćwiczenie 7.2

Załóżmy, że $f,g,h\colon[a,b]\rightarrow{\mathbb{R}}$ , przy czym $f$ i $g$ są ciągłe, a $h$ ma wahanie skończone. Udowodnij, że
a) $H(x)=\int _{a}^{x}g(t)dh(t)$ ma wahanie skończone na $[a,b]$ ,
b) $\int _{a}^{b}fdH=\int _{a}^{b}fgdh$ .

Ćwiczenie 7.3

Wykaż, że dla dowolnej funkcji ciągłej $f$ o wahaniu skończonym na $[a,b]$ zachodzi $\int _{{a}}^{{b}}f(s)df(s)=\frac{1}{2}(f^{{2}}(b)-f^{{2}}(a))$ .

Ćwiczenie 7.4

Oblicz granice w $L_{{2}}(\Omega)$ przy $n\rightarrow\infty$ ,
a) $\sum _{{k=0}}^{{n-1}}W_{{tk/n}}(W_{{t(k+1)/n}}-W_{{tk/n}})$ ,
b) $\sum _{{k=0}}^{{n-1}}W_{{t(k+1)/n}}(W_{{t(k+1)/n}}-W_{{tk/n}})$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Analizy Stochastycznej