Zagadnienia
9. Własności całki izometrycznej. Uogólnienie definicji całki stochastycznej
Poprzednio zdefiniowaliśmy całkę ![]() dla
dla ![]() . Czasami jednak
potrzeba zdefiniować całkę względem procesu Wienera z procesu ciągłego
. Czasami jednak
potrzeba zdefiniować całkę względem procesu Wienera z procesu ciągłego ![]() dla
którego
dla
którego ![]() . Podczas tego wykładu pokażemy jak określić taką
całkę.
. Podczas tego wykładu pokażemy jak określić taką
całkę.
9.1. Twierdzenie o zatrzymaniu całki stochastycznej
Zacznijmy od prostej obserwacji.
Stwierdzenie 9.1
Jeśli ![]() , to dla dowolnego
, to dla dowolnego ![]() ,
, ![]() i
i
Funkcja ![]() jest deterministyczna, więc prognozowalna,
zatem proces
jest deterministyczna, więc prognozowalna,
zatem proces ![]() jest prognozowalny jako iloczyn procesów prognozowalnych,
stąd
jest prognozowalny jako iloczyn procesów prognozowalnych,
stąd ![]() .
.
Jeśli ![]() jest procesem elementarnym postaci
jest procesem elementarnym postaci ![]() ,
to
,
to ![]() oraz
oraz
Dla ![]() weźmy
weźmy ![]() takie, że
takie, że ![]() w
w ![]() .
Wówczas oczywiście również
.
Wówczas oczywiście również ![]() w
w
![]() . Stąd
. Stąd
Uogólnieniem faktu jest ważne twierdzenie o zatrzymaniu całki stochastycznej.
Twierdzenie 9.1
Niech ![]() oraz
oraz ![]() będzie momentem zatrzymania.
Wówczas
będzie momentem zatrzymania.
Wówczas ![]() oraz
oraz
| (9.1) |
Biorąc ![]() zamiast
zamiast ![]() możemy zakładać, że
możemy zakładać, że
![]() p.n..
p.n..
Proces
![]() jest lewostronnie ciągły i adaptowalny,
a zatem jest prognozowalny, czyli
jest lewostronnie ciągły i adaptowalny,
a zatem jest prognozowalny, czyli ![]() jest prognozowalny
(iloczyn funkcji mierzalnych jest funkcją mierzalną). Stąd
jest prognozowalny
(iloczyn funkcji mierzalnych jest funkcją mierzalną). Stąd
![]() .
.
Wzór (9.1) udowodnimy w trzech krokach.
Krok 1.![]() ,
, ![]() przyjmuje skończenie wiele wartości.
przyjmuje skończenie wiele wartości.
Ewentualnie powiększając ciąg ![]() możemy zakładać, że
możemy zakładać, że ![]() przyjmuje wartości
przyjmuje wartości
![]() oraz
oraz
![]() .
Mamy
.
Mamy
![\displaystyle=\sum _{{k=0}}^{{m}}{\mathrm{I}}_{{\{\tau=t_{k}\}}}{\mathrm{I}}_{{[0,t_{k}]}}(t)=\sum _{{k=0}}^{m}\Big(\Big(\sum _{{j=0}}^{{k-1}}{\mathrm{I}}_{{\{\tau=t_{k}\}}}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}(t)\Big)+{\mathrm{I}}_{{\{\tau=t_{k}\}}}{\mathrm{I}}_{{\{ 0\}}}\Big)](wyklady/was/mi/mi1188.png) |
|||
![\displaystyle={\mathrm{I}}_{{\Omega}}{\mathrm{I}}_{{\{ 0\}}}(t)+\sum _{{j=0}}^{{m-1}}\sum _{{k=j+1}}^{m}{\mathrm{I}}_{{\{\tau=t_{k}\}}}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}(t)](wyklady/was/mi/mi1186.png) |
|||
![\displaystyle={\mathrm{I}}_{{\Omega}}{\mathrm{I}}_{{\{ 0\}}}(t)+\sum _{{j=0}}^{{m-1}}{{\mathrm{I}}_{{\{\tau>t_{j}\}}}}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}(t),](wyklady/was/mi/mi1268.png) |
zatem
![{\mathrm{I}}_{{[0,\tau]}}(t)X=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}(t)+\sum _{{j=0}}^{{m-1}}\xi _{j}{\mathrm{I}}_{{\{\tau>t_{j}\}}}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}(t),](wyklady/was/mi/mi1314.png) |
czyli ![]() . Liczymy
. Liczymy
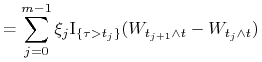 |
|||
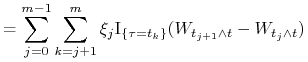 |
|||
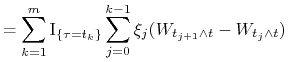 |
|||
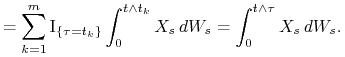 |
Krok 2.![]() dowolne oraz
dowolne oraz ![]() .
.
Weźmy ciąg momentów zatrzymania
![]() przyjmujących skończenie wiele wartości taki, że
przyjmujących skończenie wiele wartości taki, że ![]() .
Na mocy kroku 1, para
.
Na mocy kroku 1, para ![]() spełnia (9.1).
Z ciągłości trajektorii całki stochastycznej,
spełnia (9.1).
Z ciągłości trajektorii całki stochastycznej,
![]() p.n.. Mamy
p.n.. Mamy
Zbieżność wynika z twierdzenia Lebesgue'a, gdyż
proces ![]() dąży punktowo do zera i jest majoryzowany przez
dąży punktowo do zera i jest majoryzowany przez ![]() .
Stąd
.
Stąd
czyli spełnione jest (9.1).
Krok 3.![]() oraz
oraz ![]() dowolne.
dowolne.
Weźmy
![]() takie, że
takie, że ![]() w
w ![]() . Z kroku 2,
para
. Z kroku 2,
para
![]() spełnia (9.1). Mamy
spełnia (9.1). Mamy
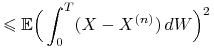 |
|||
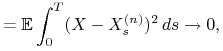 |
gdzie pierwsza nierówność wynika z nierówności Jensena oraz
Twierdzenia Dooba 6.3 dla martyngału
![]() . Ponadto
. Ponadto
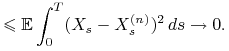 |
Stąd
czyli (9.1) spełnione jest i w tym przypadku.
∎Wniosek 9.1
Dla ![]() , proces
, proces
![]() jest martyngałem.
jest martyngałem.
Dla ![]() otrzymujemy znany fakt, że
otrzymujemy znany fakt, że ![]() jest martyngałem.
jest martyngałem.
Dowód wniosku oparty jest na następującej prostej obserwacji.
Stwierdzenie 9.2
Załóżmy, że ![]() jest adaptowalnym, prawostronnie ciągłym procesem takim, że
jest adaptowalnym, prawostronnie ciągłym procesem takim, że
![]() i dla wszystkich t,
i dla wszystkich t, ![]() . Wówczas
. Wówczas
![]() jest martyngałem wtedy i tylko wtedy gdy
jest martyngałem wtedy i tylko wtedy gdy ![]() dla wszystkich ograniczonych momentów zatrzymania
dla wszystkich ograniczonych momentów zatrzymania ![]() .
.
![]() : Z Twierdzenia Dooba 6.3,
: Z Twierdzenia Dooba 6.3, ![]() .
.
![]() : Musimy pokazać, że dla
: Musimy pokazać, że dla ![]() ,
, ![]() p.n.,
czyli
p.n.,
czyli ![]() dla wszystkich
dla wszystkich ![]() . Określmy
. Określmy
Jak łatwo sprawdzić ![]() jest momentem zatrzymania, stąd
jest momentem zatrzymania, stąd
gdzie ostatnia równość wynika z faktu, że
Dowód Wniosku
Jak wiemy ![]() , czyli proces
, czyli proces ![]() jest ciągły, adaptowalny
i całkowalny oraz
jest ciągły, adaptowalny
i całkowalny oraz ![]() . Dla ograniczonego
momentu zatrzymania
. Dla ograniczonego
momentu zatrzymania ![]() otrzymujemy na mocy twierdzenia o zatrzymaniu
całki stochastycznej
otrzymujemy na mocy twierdzenia o zatrzymaniu
całki stochastycznej
![{\mathbb{E}}\Big(\int _{{0}}^{{\tau}}X\, dW\Big)^{2}={\mathbb{E}}\Big(\int _{{0}}^{{T}}{\mathrm{I}}_{{[0,\tau]}}X\, dW\Big)^{2}={\mathbb{E}}\int _{{0}}^{{T}}{\mathrm{I}}_{{[0,\tau]}}(s)X_{s}^{2}\, ds={\mathbb{E}}\int _{{0}}^{{\tau}}X_{s}^{2}\, ds.](wyklady/was/mi/mi1239.png) |
Zatem
Teza Wniosku wynika ze Stwierdzenia 9.2.
∎9.2. Uogólnienie definicji całki stochastycznej
Definicja 9.1
Dla ![]() określamy przestrzeń procesów prognozowalnych, lokalnie
całkowalnych z kwadratem
określamy przestrzeń procesów prognozowalnych, lokalnie
całkowalnych z kwadratem
Zatem proces prognozowalny
![]() należy do przestrzeni
należy do przestrzeni ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
Przestrzeń ![]() jest liniowa, ale nie jest przestrzenią Hilberta.
jest liniowa, ale nie jest przestrzenią Hilberta.
Lemat 9.1
Dla ![]() określmy
określmy
Wówczas ![]() jest rosnącym ciagiem momentów zatrzymania,
jest rosnącym ciagiem momentów zatrzymania,
![]() p.n. Ponadto dla wszystkich
p.n. Ponadto dla wszystkich ![]() ,
,
![]() .
.
![]() jest momentem zatrzymania gdyż jest definiowany poprzez moment dojścia przez
adaptowalny proces ciągły
jest momentem zatrzymania gdyż jest definiowany poprzez moment dojścia przez
adaptowalny proces ciągły ![]() do zbioru domkniętego
do zbioru domkniętego
![]() . Z założenia o skończoności
. Z założenia o skończoności ![]() wynika, że
wynika, że
![]() p.n..
p.n..
Proces ![]() jest prognozowalny jako iloczyn procesów prognozowalnych, ponadto
na mocy nierówności Schwarza i definicji
jest prognozowalny jako iloczyn procesów prognozowalnych, ponadto
na mocy nierówności Schwarza i definicji ![]() ,
,
![{\mathbb{E}}\Big(\int _{0}^{T}{\mathrm{I}}_{{[0,\tau _{n}]}}(s)X_{s}\, ds\Big)^{2}={\mathbb{E}}\Big(\int _{0}^{{\tau _{n}}}X_{s}\, ds\Big)^{2}\leq{\mathbb{E}}\Big[\tau _{n}\int _{0}^{{\tau _{n}}}X_{s}^{2}\, ds\Big]\leq n^{2}<\infty.](wyklady/was/mi/mi1287.png) |
Załóżmy, że mamy dany rosnący ciąg momentów zatrzymania ![]() p.n.
taki, że
p.n.
taki, że ![]() dla wszystkich
dla wszystkich ![]() .
Niech
.
Niech ![]() . Przypomnijmy też,
że przez
. Przypomnijmy też,
że przez ![]() oznaczamy proces
oznaczamy proces ![]() zatrzymany w chwili
zatrzymany w chwili ![]() (zob.
Definicja 4.9).
(zob.
Definicja 4.9).
Lemat 9.2
Dla ![]() , procesy
, procesy
![]() i
i ![]() są nierozróżnialne, czyli
są nierozróżnialne, czyli
Na mocy twierdzenia o zatrzymaniu całki stochastycznej dla ustalonego ![]() ,
,
Zatem ![]() jest modyfikacją
jest modyfikacją ![]() .
Teza lematu wynika z ciągłości obu procesów.
.
Teza lematu wynika z ciągłości obu procesów.
Definicja 9.2
Niech ![]() oraz
oraz ![]() będzie rosnącym do
będzie rosnącym do ![]() ciągiem momentów zatrzymania
takich, że
ciągiem momentów zatrzymania
takich, że ![]() dla wszystkich
dla wszystkich ![]() .
Całką stochastyczną
.
Całką stochastyczną
![]() dla
dla ![]() nazywamy taki
proces
nazywamy taki
proces ![]() , że
, że
![]() dla
dla ![]() .
.
Stwierdzenie 9.3
Proces ![]() zdefiniowany powyżej jest jest ciągły i jednoznacznie określony w klasie
procesów nieodróżnialnych.
zdefiniowany powyżej jest jest ciągły i jednoznacznie określony w klasie
procesów nieodróżnialnych.
Na mocy Lematu 9.2 dla każdego ![]() istnieje zbiór
istnieje zbiór
![]() taki, że
taki, że ![]() oraz dla
oraz dla ![]() zachodzi
zachodzi
![]() dla wszystkich
dla wszystkich ![]() .
Niech
.
Niech ![]() , wówczas
, wówczas ![]() oraz dla
oraz dla
![]() ,
, ![]() ciąg
ciąg ![]() jest stały. Zatem możemy (i musimy) położyć
jest stały. Zatem możemy (i musimy) położyć
![]() dla
dla ![]() .
.
Stwierdzenie 9.4
Definicja
![]() nie zależy od wyboru ciągu
nie zależy od wyboru ciągu ![]() dla
dla ![]() .
Dokładniej, jeśli
.
Dokładniej, jeśli
![]() ,
, ![]() - momenty zatrzymania,
- momenty zatrzymania, ![]() ,
,
![]() ,
, ![]() i
i
![]() oraz
oraz
![]() określone jak w Definicji 9.2 za pomocą
określone jak w Definicji 9.2 za pomocą
![]() ,
, ![]() odpowiednio,
to procesy
odpowiednio,
to procesy ![]() i
i ![]() są nierozróżnialne.
są nierozróżnialne.
Mamy
Na mocy twierdzenia o zatrzymaniu całki stochastycznej,
Ponadto ![]() , więc
, więc
![]() dla
dla ![]() i stąd
i stąd ![]() p.n.,
a że są to procesy ciągłe, to są nierozróżnialne.
p.n.,
a że są to procesy ciągłe, to są nierozróżnialne.
Sformułujemy teraz uogólnienie twierdzenia o zatrzymaniu całki stochastycznej.
Twierdzenie 9.2
Jeśli ![]() , to dla dowolnego momentu zatrzymania
, to dla dowolnego momentu zatrzymania ![]() ,
,
![]() oraz
oraz
Proces ![]() jest prognozowalny jako iloczyn
procesów prognozowalnych, jest majoryzowany przez
jest prognozowalny jako iloczyn
procesów prognozowalnych, jest majoryzowany przez ![]() , stąd
, stąd ![]() .
Proces
.
Proces ![]() , więc istnieje ciąg
, więc istnieje ciąg
![]() taki, że
taki, że ![]() . Wtedy
też
. Wtedy
też ![]() .
Niech
.
Niech
Na mocy definicji,
Z udowodnionego wcześniej Twierdzenia 9.1 o zatrzymaniu całki izometrycznej,
Biorąc ![]() dostajemy
dostajemy
![]() , czyli
, czyli
![]() .
.
9.3. Martyngały lokalne
Definicja 9.3
Jeżeli dla procesu adaptowalnego ![]() , istnieje ciąg
momentów zatrzymania
, istnieje ciąg
momentów zatrzymania ![]() taki, że
taki, że ![]() jest martyngałem, to
jest martyngałem, to ![]() nazywamy martyngałem lokalnym.
Jeśli dodatkowo
nazywamy martyngałem lokalnym.
Jeśli dodatkowo ![]() , to mówimy, że
, to mówimy, że
![]() jest ciągłym martyngałem lokalnym całkowalnym
z kwadratem. Klasę takich procesów oznaczamy
jest ciągłym martyngałem lokalnym całkowalnym
z kwadratem. Klasę takich procesów oznaczamy
![]() (
(![]() jeśli wartość
jeśli wartość ![]() jest jasna
z kontekstu).
jest jasna
z kontekstu).
Uwaga 9.1
![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
![]() ,
gdzie
,
gdzie ![]() oznacza rodzinę ciągłych martyngałów lokalnych.
oznacza rodzinę ciągłych martyngałów lokalnych.
Stwierdzenie 9.5
Załóżmy, że ![]() dla
dla ![]() .
Wówczas
.
Wówczas
i) ![]() jest procesem ciągłym,
jest procesem ciągłym, ![]() ,
,
ii) ![]() ,
,
iii) Przekształcenie ![]() jest liniowe.
jest liniowe.
Punkty i), ii) wynikają z definicji. By udowodnić iii) weźmy
![]() . Istnieją wówczas momenty zatrzymania
. Istnieją wówczas momenty zatrzymania ![]() i
i ![]() takie, że
takie, że ![]() oraz
oraz ![]() . Przyjmując
. Przyjmując
![]() otrzymujemy
otrzymujemy
![]() ,
a zatem
,
a zatem ![]() dla dowolnych
dla dowolnych
![]() . Stąd na mocy definicji otrzymujemy, że
. Stąd na mocy definicji otrzymujemy, że
![]() i
biorąc granicę
i
biorąc granicę ![]() ,
,
![]()
Uwaga 9.2
Martyngał lokalny ![]() dla
dla ![]() nie musi być martyngałem,
nie musi być martyngałem,
![]() nie musi
być nawet całkowalne. Ale, jeśli
nie musi
być nawet całkowalne. Ale, jeśli ![]() dla wszystkich
dla wszystkich
![]() , to
, to ![]() jest martyngałem, bo możemy przyjąć
jest martyngałem, bo możemy przyjąć ![]() , gdzie
, gdzie
![]() jest ciągiem rosnącym zbieżnym do
jest ciągiem rosnącym zbieżnym do ![]() i wtedy
i wtedy
![]() .
.
Uwaga 9.3
Przykłady ciągłych martyngałów lokalnych, które nie są martyngałami są podane w Ćwiczeniach 13.4 i 13.6.
Mimo, że w przypadku ogólnym ![]() nie musi być martyngałem, to zachodzi
dla tego procesu nierówność Dooba.
nie musi być martyngałem, to zachodzi
dla tego procesu nierówność Dooba.
Twierdzenie 9.3 (Nierówność Dooba)
Dla dowolnego procesu ![]() oraz momentu
zatrzymania
oraz momentu
zatrzymania ![]() ,
,
Weźmy ![]() takie, że
takie, że ![]() .
Mamy
.
Mamy
![\displaystyle={\mathbb{E}}\sup _{{t<T}}\Big(\int _{0}^{{t\wedge\tau}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2}={\mathbb{E}}\sup _{{t\leq T}}\Big(\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2},](wyklady/was/mi/mi1201.png) |
![]() , więc
, więc ![]() można zamienić na
można zamienić na ![]() .
Na mocy nierówności Dooba dla martyngałów,
.
Na mocy nierówności Dooba dla martyngałów,
![\displaystyle{\mathbb{E}}\sup _{{t\leq T}}\Big(\int _{0}^{t}{\mathrm{I}}_{{[0,T]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2}](wyklady/was/mi/mi1223.png) |
![\displaystyle\leq 4{\mathbb{E}}\Big(\int _{0}^{T}{\mathrm{I}}_{{[0,\tau]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2}](wyklady/was/mi/mi1293.png) |
||
![\displaystyle=4{\mathbb{E}}\int _{0}^{T}({\mathrm{I}}_{{[0,\tau]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X_{s})^{2}\, ds=4{\mathbb{E}}\int _{0}^{{\tau\wedge\tau _{n}}}X_{s}^{2}\, ds](wyklady/was/mi/mi1246.png) |
|||
Wykazaliśmy zatem, że
Ponieważ
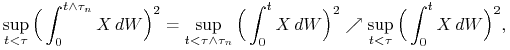 |
więc teza wynika z twierdzenia Lebesgue'a o zbieżności monotonicznej.
∎Stwierdzenie 9.6
a) Każdy ograniczony martyngał lokalny jest martyngałem.
b) Każdy nieujemny martyngał lokalny jest
nadmartyngałem.
Załóżmy, że ![]() jest ciągiem momentów zatrzymania takim, że
dla każdego
jest ciągiem momentów zatrzymania takim, że
dla każdego ![]() ,
, ![]() jest martyngałem. Ustalmy
jest martyngałem. Ustalmy ![]() oraz
oraz ![]() .
.
a) Jeśli ![]() jest ograniczony, to z twierdzenia Lebesgue'a o zbieżności zmajoryzowanej,
jest ograniczony, to z twierdzenia Lebesgue'a o zbieżności zmajoryzowanej,
stąd ![]() jest martyngałem.
jest martyngałem.
b) Jeśli ![]() jest nieujemny, to
jest nieujemny, to
gdzie korzystaliśmy z twierdzenia Lebesgue'a o zbieżności monotonicznej,
tego, że ![]() jest martyngałem i
jest martyngałem i ![]() oraz z lematu Fatou.
oraz z lematu Fatou.
9.4. Zadania
Ćwiczenie 9.1
Niech ![]() będzie momentem zatrzymania takim, że
będzie momentem zatrzymania takim, że ![]() .
Wykaż, że
.
Wykaż, że ![]() oraz
oraz
![]() . Wywnioskuj stąd, że
. Wywnioskuj stąd, że
![]() oraz
oraz ![]() .
.
Ćwiczenie 9.2
Dla ![]() określmy
określmy ![]() . Wykaż, że
. Wykaż, że
![]() p.n. oraz
p.n. oraz ![]() wtedy i tylko wtedy gdy
wtedy i tylko wtedy gdy ![]() .
Ponadto dla
.
Ponadto dla ![]() ,
, ![]() .
.
Ćwiczenie 9.3
Wykaż, że dla ![]() ,
, ![]() jest
ciągłym martyngałem lokalnym.
jest
ciągłym martyngałem lokalnym.
Ćwiczenie 9.4
Niech ![]() ,
, ![]() oraz
oraz ![]() będzie zmienną losową
będzie zmienną losową ![]() -mierzalną (niekoniecznie ograniczoną).
Wykaż, że
-mierzalną (niekoniecznie ograniczoną).
Wykaż, że ![]() oraz
oraz
![]() .
.
Ćwiczenie 9.5
Znajdź proces ![]() taki, że
taki, że ![]() nie
jest martyngałem.
nie
jest martyngałem.
Ćwiczenie 9.6
Wykaż, że ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
![]() .
.
Ćwiczenie 9.7
Niech ![]() będzie martyngałem lokalnym takim, że
będzie martyngałem lokalnym takim, że ![]() dla wszystkich
dla wszystkich ![]() oraz
oraz ![]() . Wykaż, że
. Wykaż, że ![]() jest martyngałem.
jest martyngałem.
Ćwiczenie 9.8
Podaj przykład nieujemnego całkowalnego ciągłego martyngału lokalnego, który nie jest martyngałem.




