Zagadnienia

3.1 Definicje
3.2 Własności RN

3. Równowaga Nasha

3.1. Definicje

Równowaga Nasha (RN) jest centralnym pojęciem teorii gier strategicznych.

Definicja (ważna) 3.1

Profil (strategii mieszanych) gry strategicznej $\sigma^{*}$ jest równowagą Nasha wtedy i tylko wtedy jeżeli

$u_{i}(\sigma^{*}_{i},\sigma^{*}_{{-i}})\ge u_{i}(\sigma _{i},\sigma^{*}_{{-i}})\quad\forall i=1,...n,\ \forall\sigma _{i}\in\Sigma _{i}$

Słownie: żaden z graczy nie może podwyższyć swojej wypłaty przez jednostronną (to znaczy bez zmiany strategii wszystkich innych graczy) zmianę swojej strategii.

W dalszym ciągu udowodnimy ważne twierdzenia charakteryzujące RN.

3.2. Własności RN

Definicja 3.2

Nośnik strategii mieszanej $\sigma _{i}=(\sigma _{{i1}},...,\sigma _{{im_{i}}})$ jest to zbiór $supp\sigma _{i}\subset A_{i}$ akcji (strategii czystych gracza $i$ ) taki że akcja o numerze $k$ z $A_{i}$ należy do $supp\sigma _{i}\ \Leftrightarrow\sigma _{{ik}}>0$ .

INaczej mówiąc nosnik strategii $\sigma _{i}$ jest to zbiór strategii czystych które sa grane z dodatnimi prawdopodobieństwami w danej strategii mieszanej $\sigma _{i}$ .

Jeżeli używamy dla strategii mieszanej notacji $x_{i}$ , to jej nośnik oznaczmy $suppx_{i}$ . Nośnik strategii czystej jest singletonem. Można wprowadzić dodatkowe charakterystyki strategii: strategie istotnie mieszane (te które nie są czyste) i całkowicie mieszane (te których nośniki pokrywają się ze odpowiednim zbiorem strategii czystych).

Twierdzenie 3.1 (O wypłatach strategii czystych w RN)

Niech

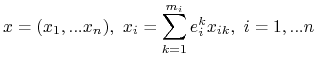$x=(x_{1},...x_{n}),\ x_{i}=\sum _{{k=1}}^{{m_{i}}}e_{i}^{k}x_{{ik}},\ i=1,...n$

- profil strategii mieszanych GS. Ustalmy gracza $i$ . Niech $e_{i}^{{k_{1}}},e_{i}^{{k_{2}}}$ - dwie różne strategie w $suppx_{i}$ czyli $p_{1}:=x_{{ik_{1}}}>0,\ p_{2}:=x_{{ik_{2}}}>0$ . Wtedy

$x\ jest\ RN\Rightarrow\forall i\in N\ \ u_{i}(e_{i}^{{k_{1}}},x_{{-i}})=u_{i}(e_{i}^{{k_{2}}},x_{{-i}})$

(3.1)

Tak więc w RN każdy gracz ma jednakowe wypłaty ze wszystkich strategii czystych z nośnika swojej strategii mieszanej którą gra w RN.

Uwaga 3.1

$u_{i}(e_{i}^{{k_{1}}},x_{{-i}})$ oznacza $u_{i}(x_{1},x_{2},...,e_{i}^{{k_{1}}},...,,x_{{n}})$ .

ad absurdum. Niech $x=(x_{1},...,x_{n})$ - RN, oraz

$\displaystyle u_{i}(e_{i}^{{k_{1}}},x_{{-i}})>u_{i}(e_{i}^{{k_{2}}},x_{{-i}})$

(3.2)

Definiujemy profil

$\tilde{x}=(x_{1},...,x_{{i-1}},\tilde{x}_{i},x_{{i+1}},...,x_{N})$

taki że

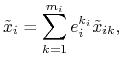$\tilde{x}_{i}=\sum _{{k=1}}^{{m_{i}}}e_{i}^{{k_{i}}}\tilde{x}_{{ik}},$

gdzie

$\tilde{x}_{{ik_{1}}}=p_{1}+p_{2},$

$\tilde{x}_{{ik_{2}}}=0,$

$\tilde{x}_{{ij}}=x_{{ij}}\ \ dla\ \ j\neq k_{1},j\neq k_{2}.$

Pokażemy że

$\displaystyle u_{i}(\tilde{x}_{i},x_{{-i}})>u_{i}(x_{i},x_{{-i}})$

(3.3)

czyli sprzeczność z definicją RN. Lewa strona tej nierówności ma postać:

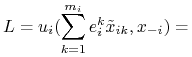	$\displaystyle L=u_{i}(\sum _{{k=1}}^{{m_{i}}}e_{i}^{k}\tilde{x}_{{ik}},x_{{-i}})=$	$\displaystyle(p_{1}+p_{2})u_{i}(e_{i}^{{k_{1}}},x_{{-i}})$		(3.4)
		$\displaystyle+0\cdot u_{i}(e_{i}^{{k_{2}}},x_{{-i}})+u_{i}(\sum _{{k\neq k_{1},k\neq k_{2}}}e_{i}^{k}x_{{ik}},x_{{-i}}).$		(3.5)

Prawa strona nierówności

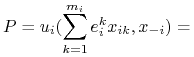	$\displaystyle P=u_{i}(\sum _{{k=1}}^{{m_{i}}}e_{i}^{k}x_{{ik}},x_{{-i}})=$	$\displaystyle p_{1}u_{i}(e_{i}^{{k_{1}}},x_{{-i}})+p_{2}u_{i}(e_{i}^{{k_{2}}},x_{{-i}})$		(3.6)
		$\displaystyle+u_{i}(\sum _{{k\neq k_{1},k\neq k_{2}}}e_{i}^{k}x_{{ik}},x_{{-i}}),$		(3.7)

a zatem z (3.2) otrzymujemy $L>P$ , czyli (3.3), i.e. sprzeczność z definicją RN.

∎

Wniosek 3.1

Wypłata każdego gracza w RN jest równa jego wypłacie z profilu w którym gracz ten gra dowolną strategią czystą z nośnika swojej strategii w RN, a pozostali gracze grają swoimi strategiami z RN. Mowi o tym

Stwierdzenie 3.1 (O wypłatach w RN)

Niech

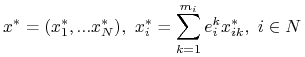$x^{*}=(x_{1}^{*},...x_{N}^{*}),\ x_{i}^{*}=\sum _{{k=1}}^{{m_{i}}}e_{i}^{k}x_{{ik}}^{*},\ i\in N$

- profil strategii mieszanych GS w RN. Wypłata każdego gracza $i\in N$ z profilu $x^{*}$ jest równa jego wypłacie z profilu w którym gra (dowolną) strategię czystą z $suppx_{i}^{*}$ a wszyscy inni nie zmieniają swych strategii. Formalnie:

$u_{i}(x_{i}^{*},x_{{-i}}^{*})=u_{i}(e_{i}^{k},x_{{-i}}^{*})\quad\forall e_{i}^{k}\in suppx_{i}^{*}$

(3.8)

Mówimy, że w RN wypłata gracza jest równa wypłacie z dowolnej granej przez niego w RN strategii czystej.

Gracz $i$ gra w RN pewną strategią $x_{i}^{*}=\sum _{{k\in suppx_{i}^{*}}}x_{{ik}}^{*}e_{i}^{k}.$

Korzystając z liniowości $u_{i}$ otrzymujemy

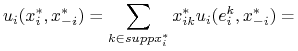$u_{i}(x_{i}^{*},x_{{-i}}^{*})=\sum _{{k\in suppx_{i}^{*}}}x_{{ik}}^{*}u_{i}(e_{i}^{k},x_{{-i}}^{*})=$

(z Twierdzenia 3.1), oznaczając $s$ –numer dowolnej ustalonej strategii z $suppx_{i}^{*}$ :

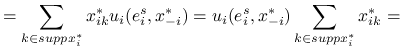$=\sum _{{k\in suppx_{i}^{*}}}x_{{ik}}^{*}u_{i}(e_{i}^{s},x_{{-i}}^{*})=u_{i}(e_{i}^{s},x_{{-i}}^{*})\sum _{{k\in suppx_{i}^{*}}}x_{{ik}}^{*}=$

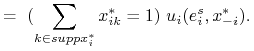$=\ (\sum _{{k\in suppx_{i}^{*}}}x_{{ik}}^{*}=1)\ u_{i}(e_{i}^{s},x_{{-i}}^{*}).$

∎

Poniżej udowodnimy twierdzenie które pozwala znaleźć RN jeśli jest spełniony warunek dostateczny, oraz daje charakterystykę RN jako warunek konieczny.

$\$

$\Rightarrow$ :

Warunek 1. jest identyczny z Twierdzeniem 3.1.

Warunek 2.: ad absurdum: w przeciwnym razie mielibyśmy

$u_{i}(s^{{\prime}},x_{{-i}}^{*})>u_{i}(s^{{\prime\prime}},x_{{-i}}^{*})\ \ dla\ \ s^{{\prime}}\notin suppx_{i}^{*},s^{{\prime\prime}}\in suppx_{i}^{*}.$

Z Wniosku (3.1), w RN dla $s^{{\prime\prime}}\in suppx_{i}^{*}$

$u_{i}(s^{{\prime\prime}},x_{{-i}}^{*})=u_{i}(x_{i}^{*},x_{{-i}}^{*})\equiv u_{i}(x^{*}),$

a zatem otrzymujemy $u_{i}(s^{{\prime}},x_{{-i}}^{*})>u_{i}(x_{i}^{{*}},x_{{-i}}^{*})$ , sprzeczność z definicją RN.

$\Leftarrow$ :

Ustalmy gracza $i$ . Niech $x_{i}^{*}$ będzie jego strategią mieszaną spełniającą warunki 1. i 2. Należy wykazać że

$u_{i}(x_{i},x_{{-i}}^{*})\le u_{i}(x_{i}^{*},x_{{-i}}^{*})\ \ \forall x_{i}\in\Sigma _{i}.$

Oznaczmy, pomijając dla uproszczenia notacji w obu symbolach indeks $i$ : $\ S:=suppx_{i}^{*}$ , $\ a_{k}\equiv e_{i}^{k}$ - k-ta strategia czysta gracza $i$ . Rozkładając $u_{i}(x_{i},x_{{-i}}^{*})$ względem nośnika strategii $x_{i}^{*}$ i jego dopełnienia otrzymujemy, korzystając z liniowości $u_{i}$ :

$u_{i}(x_{i},x_{{-i}}^{*})=\sum _{{a_{k}\in S}}x_{{ik}}u_{i}(a_{k},x_{{-i}}^{*})+\sum _{{a_{k}\notin S}}x_{{ik}}u_{i}(a_{k},x_{{-i}}^{*}),$

gdzie zastosowaliśmy zapis $x_{i}=\sum _{{k}}a_{k}x_{{ik}}.$

Pierwsza suma po prawej stronie ma (z warunku 1.) postać:

$\sum _{{a_{k}\in S}}x_{{ik}}u_{i}(a_{s},x_{{-i}}^{*})=u_{i}(a_{s},x_{{-i}}^{*})\sum _{{a_{k}\in S}}x_{{ik}},$

gdzie $a_{s}$ jest jedną ze strategii czystych z nośnika $S$ . Druga suma spełnia (z warunku 2.) nierówność:

$\sum _{{a_{k}\notin S}}x_{{ik}}u_{i}(a_{k},x_{{-i}}^{*})\le\sum _{{a_{k}\notin S}}x_{{ik}}u_{i}(a_{s},x_{{-i}}^{*})=u_{i}(a_{s},x_{{-i}}^{*})\sum _{{a_{k}\notin S}}x_{{ik}}$

gdzie $a_{s}$ jest ustaloną strategią czystą z nośnika $S$ . Zatem, ponieważ $A_{i}=S\cup\bar{S}$ ,

$u_{i}(x_{i},x_{{-i}}^{*})\le u_{i}(a_{s},x_{{-i}}^{*})\sum _{{a_{k}\in A_{i}}}x_{{ik}},$

Zauważmy że dla obu profili $x_{i}$ oraz $x_{i}^{*}$ (każdy profil należy do sympleksu jednostkowego $\Delta _{i}$ )

$\sum _{{a_{k}\in A_{i}}}x_{{ik}}=\sum _{{a_{k}\in A_{i}}}x_{{ik}}^{*}=1,$

a więc

$u_{i}(x_{i},x_{{-i}}^{*})\le u_{i}(a_{s},x_{{-i}}^{*})\sum _{{a_{k}\in A_{i}}}x_{{ik}}^{*}=\sum _{{a_{k}\in S}}u_{i}(a_{s},x_{{-i}}^{*})x_{{ik}}^{*}+\sum _{{a_{k}\notin S}}u_{i}(a_{s},x_{{-i}}^{*})x_{{ik}}^{*}.$

Wykorzystując warunek 1. (do zamiany $a_{s}$ na $a_{k}$ ), reprezentację $x_{i}^{*}=\sum _{{a_{k}\in A_{i}}}a_{k}x_{{ik}}^{*}$ i liniowość funkcji wypłat względem odpowiednich argunentów, przepisujemy wyrażenie po ostatnim znaku równości w postaci

$\sum _{{a_{k}\in S}}u_{i}(a_{k},x_{{-i}}^{*})x_{{ik}}^{*}+\sum _{{a_{k}\notin S}}u_{i}(a_{s},x_{{-i}}^{*})x_{{ik}}^{*}=\sum _{{a_{k}\in A_{i}}}u_{i}(a_{k},x_{{-i}}^{*})x_{{ik}}^{*}=u_{i}(x_{i}^{*},x_{{-i}}^{*}),$

gdzie ostatnia równość wynika z liniowości wypłat. Otrzymaliśmy więc

$u_{i}(x_{i},x_{{-i}}^{*})\le u_{i}(x_{i}^{*},x_{{-i}}^{*}).$

Powyższe rozumowanie przeprowadzamy $\forall i\in N$ .

∎

Pokażemy przykład zastosowania Twierdzenia LABEL:waz1.

Przykład 3.1

$\$

	L	C	R
T	$a$ ,2	3,3	1,1
M	0,0	0,0	2, $b$
B	$c$ ,4	5,1	0, 7

$a,b,c\in\Re$ . Nastepująca para (profil) strategii mieszanych jest RN:

$x^{*}=(x_{1}^{*},x_{2}^{*})=((3/4,0,1/4),(0,1/3,2/3))$

Porównamy wypłaty ze strategii czystych i zastosujemy Twierdzenie LABEL:waz1. Obliczamy wypłaty ze strategii czystych gdy profil przeciwnika jest z RN. Dla gracza $i=1$ :

Wypłata z $T:0\cdot a+1/3\cdot 3+2/3\cdot 1=5/3$

Wypłata z $M:0\cdot b+1/3\cdot 0+2/3\cdot 2=4/3$

Wypłata z $B:0\cdot c+1/3\cdot 5+2/3\cdot 0=5/3$

Wypłaty ze strategii czystych z $suppx_{1}=\{ T,B\}$ są jednakowe, wypłata z $M$ jest niższa. Dla gracza $i=2$ analogiczny rachunek pokazuje że wypłaty ze wszystkich strategii czystych: $u_{2}(x_{1}^{*},\cdot)$ są równe $5/2$ , np:

$u_{2}(x_{1}^{*},L)=2\cdot 3/4+0\cdot 0+4\cdot 1/4=5/2.$

Warunki dostateczne na RN (dla drugiego gracza jest potrzebny tylko warunek 1) są więc spełnione.

∎

Uwaga: Jeśli w drugim wierszu zamienimy 2 na 3 to powyższy profil nie będzie RN bo

$u_{1}((M,x_{2}^{*}))=u_{1}((0,1,0),(0,1/3,2/3))=6/3>5/3.$

A oto jeszcze jedna charakterystyka RN dająca w szczególności warunek dostateczny istnienia RN.

Stwierdzenie 3.2

Profil $x^{*}$ jest RN $\Leftrightarrow$

$\forall i\in N,\forall e_{i}^{k}\in A_{i}\ \ u_{i}(e_{i}^{k},x_{{-i}}^{*})\le u_{i}(x_{i}^{*},x_{{-i}}^{*})$

$\$

$\Rightarrow$ : Z definicji RN.

$\Leftarrow$ : Ustalmy $i$ . Niech $x_{i}=\sum _{{k=1}}^{{m_{i}}}x_{{ik}}e_{i}^{k}$ - dowolna strategia mieszana gracza $i$ . Obliczamy: z liniowości

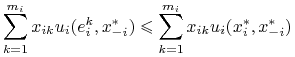	$\displaystyle u_{i}(x_{i},x_{{-i}}^{*})=$	$\displaystyle\sum _{{k=1}}^{{m_{i}}}x_{{ik}}u_{i}(e_{i}^{k},x_{{-i}}^{})\le\sum _{{k=1}}^{{m_{i}}}x_{{ik}}u_{i}(x_{i}^{},x_{{-i}}^{*})$		(3.9)
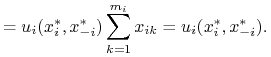		$\displaystyle=u_{i}(x_{i}^{},x_{{-i}}^{})\sum _{{k=1}}^{{m_{i}}}x_{{ik}}=u_{i}(x_{i}^{},x_{{-i}}^{}).$		(3.10)

∎

Istotną rolę w teorii gier strategicznych odgrywa ścisła RN.

Definicja 3.3

Profil $x^{*}=(x_{1}^{*},...,x_{i}^{*})$ jest ścisłą RN (SRN) $\Leftrightarrow\forall i\ \ \forall x_{i}\ne x_{i}^{*}$

$u_{i}(x_{i},x_{{-i}}^{*})<u_{i}(x_{i}^{*},x_{{-i}}^{*})$

Uwaga 3.2

RN jest SRN gdy strategia każdego gracza w RN jest JEDYNĄ najlepszą odpowiedzią na strategie wszystkich innych graczy w RN (definicja najlepszej odpowiedzi będzie podana w następnym rozdziale).

Mówimy że skończona GS jest generyczna jeśli $\forall i\in N$ funkcja wypłat $u_{i}$ jest różnowartościowa.

Zachodzi:

Stwierdzenie 3.3

SRN jest RN w strategiach czystych

Wsk. W przeciwnym razie w RN nośnik strategii $x_{i}$ pewnego gracza $i$ nie jest singletonem. Z Twierdzenia 3.1 wynika istnienie co najmniej dwóch różnych najlepszych odpowiedzi na $x_{i}$ .

∎

Uwaga 3.3

SRN nie musi istnieć. Przykład: Gra Orzeł-Reszka.

RN w strategiach czystych nie musi być SRN. Przykład: W grze

	A	B
A	1,1	0,0
B	0,0	0,0

(A,A) jest SRN, (B,B) nie.

Nawet gdy GS ma dokładnie jedną RN, to ta RN nie musi być SRN. Przykład: w grze

	A	B	C
D	1,1	1,0	0,1
E	1,0	0,1	1,0

$(D,A)$ jest (jedyną) RN, ale nie jest SRN.

Przykład 3.2

W Słabym Dylemacie Więźnia nie ma SRN. To że mieszane strategie nie są SRN wynika ze Stwierdzeniaq 3.3. Bezpośredni rachunek pokazuje że żadna z 3 czystych Rn nie jest SRN.

Definicja 3.4

Profil $\sigma^{*}=(\sigma _{j}^{*})_{{j\in N}}$ w GS w której wszyscy gracze mają ten sam zbiór akcji ( czyli $A_{j}=A,\ \forall j\in N$ ) jest symetryczną RN jeśli jest RN oraz $\sigma _{i}^{*}=\sigma _{j}^{*}\ \ \forall i,j\in A.$

Uwaga 3.4

”Większość” gier skończonych ma nieparzystą liczbę RN. Przykładem sa gry 2–osobowe dla których $\forall i\in N$ funkcja $u_{i}:A\rightarrow\Re$ jest różnowartościowa (gry generyczne).

Oto ”kontrprzykład”: GS z czterema RN ([33]):

	A	B	C
D	0,0	-1,-1	-1,-1
E	-1,-1	-1,-1	-1,-1
E	-1,-1	-1,-1	0,0

(poza trzema czystymi RN jest ”częściowo mieszana” RN $(1/2,0,1/2)$ .

Innym ”kontrprzykładem” jest gra ”Słaby Dylemat Więźnia”, która jest modyfikacją DW z wypłatą $P=S$ :

	C	D
C	R,R	S,T
D	T,S	S,S

dla $T>R>S$ . Wypłata każdego gracza nie jest funkcją różnowartośiowa. Gra ma continuum RN (w tym 3 RN w strategiach czystych), patrz Cwiczenie 4.1.

W ekonomicznych zastosowaniach teorii gier istotną rolę odgrywa pojęcie Pareto-optymalności.

Definicja 3.5

Profil gry strategicznej jest Pareto-optymalny (PO) jeżeli nie istnieje profil dający conajmniej jednemu graczowi wyższą, a wszystkim innym conajmniej taką samą wypłatę.

Profil gry jest Pareto-nieoptymalny jeżeli istnieje inny, lepszy dla conajmniej jednego gracza i nie gorszy dla żadnego (czyli gdy nie jest PO).

Przykład 3.3

$\$

	L	S	R
U	4,3	5,1	6,2
M	2,1	8,4	3,6
D	3,0	9,6	2,8

$(U,L)$ jest RN ale nie jest PO. $(D,S)$ jest PO, ale nie jest RN.

Przykład 3.4

Gra koordynacyjna

	A	B
A	2,2	$-10^{{-5}}$ ,0
B	$-10^{{-5}}$ ,0	1,1

ma 2 RN w strategiach czystych. RN (A,A) jest PO, ale, zakładając wypłaty np. w PLN, nie jest to ”przekonywujący” wybór w praktycznej realizacji.

Przykład 3.5

W 2-osobowym DW profil (C,C) jest PO gdyż gdy jeden z graczy sobie podwyższy wypłatę to wypłata drugiego się obniży. (C,C) jest PO, ale nie jest RN. Profil (D,D) jest RN ale nie jest PO.

W ”Dylemacie Wspólnych Zasobów” (Tragedy of Commons) tzw. minimalna efektywna kooperacja (czyli profil w którym jest dokładnie tylu kooperantów ile wynosi ”próg” - minimalna liczba kooperantów przy której pula jest rozdzielana między wszystkich graczy) jest jedynym profilem PO.

Dla gier o sumie stałej (patrz część 5) każdy profil jest PO (bo nie istnieje profil dający conajmniej jednemu graczowi wyższą, a wszystkim innym conajmniej taką samą wypłatę).

Ćwiczenie 3.1

Pokazać że DW nie ma innych równowag poza (D,D).

W strategiach czystych nie ma innych RN poza (D,D). Gdyby miał równowagę ściśle mieszaną $(\sigma _{1},\sigma _{2})$ , to dla $\sigma _{2}=(\beta,1-\beta)$ mamy, z twierdzenia podstawowego $u_{1}(C,\sigma _{2})=u_{1}(D,\sigma _{2})$ , czyli $R\beta+S(1-\beta)=T\beta+P(1-\beta)$ , czyli $(S-P)(1-\beta)=(T-R)\beta$ , sprzeczność dla DW. Dla profili w których jeden gracz gra strategią ściśle mieszaną a drugi czystą z twierdzenia–warunku koniecznego na wypłaty z obu strategii czystych pierwszego gracza byłyby jednakowe, co nie jest możliwe dla DW.

Ćwiczenie 3.2

Pokaż że w grze w Kota i Myszkę $u_{M}((1/2,1/2),(1/2,1/2))\ge u_{M}((x,1-x),(1/2,1/2))\ \ \forall x\in[0,1],$ oraz $u_{M}((1/2,1/2),(1/2,1/2))\ge u_{M}((1/2,1/2),(y,1-y))\ \ \forall y\in[0,1],$ a zatem para strategii $((1/2,1/2),(1/2,1/2))$ jest RN (w istocie zachodzą równości).

Ćwiczenie 3.3

Ogólniejsza postać gry ”W Kota i Myszkę”

	L	P
L	0,K	M,0
P	M,0	0,K

Obliczyć średnie wypłaty przy stosowaniu strategii mieszanych i znależć RN.

Ćwiczenie 3.4

W grze

	L	S	R
U	0,1	0,1	2,4
M	5,1	2,2	1,0
D	4,3	1,4	1,0

znależć RN i profile PO w strategiach czystych.

Odp.: (U,R): RN, PO. (M,S):RN ale nie PO. (D,L):PO ale nie RN.

Ćwiczenie 3.5

Znaleźć RN w grze

	L	S	R
U	1,3	1,3	1,3
M	0,0	2,2	2,2
D	0,0	0,0	3,1

Ćwiczenie 3.6

GS jest o sumie zerowej jeżeli $\forall(a_{1},...,a_{n})\in A\ \sum _{{i=1}}^{n}u_{i}(a_{1},...,a_{n})=0$ . Wykaż że dla GS o sumie zerowej każdy profil jest PO.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Teorii Gier