Zagadnienia

5.1 Definicje
5.2 Własności. Podstawowe twierdzenia

5. Gry o sumie zerowej

Dwuosobowe gry o sumie zerowej (ogólniej: o sumie stałej) byly–chronologicznie–pierwszym typem gier rozważanym przez natematyków, w szczególności w pracach J. von Neumanna w latach 20ych i 30ych XX wieku. Gry o sumie zerowej były podstawą opracowanej przez J. von Neumanna i O. Morgensterna matematycznej teorii gier [16].

5.1. Definicje

Definicja 5.1

GS jest grą o sumie stałej jeżeli

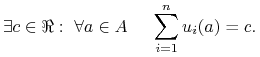$\exists c\in\Re:\ \forall a\in A\ \quad\sum _{{i=1}}^{n}u_{i}(a)=c.$

Jeśli $c=0$ to GS nazywamy grą o zumie zerowej i oznaczamy GS0.

Gry dwuosobowe (n=2) o sumie zero nazywa się też grami ściśle konkurencyjnymi. Nazwa gry ściśle konkurencyjne wynika stąd że w takich grach interesy graczy są ”ściśle przeciwstawne”: aby uzyskać maksymalną wypłatę gracz dąży do tego by zminimalizować sumę wypłat przeciwników. W takich grach gracze mają przeciwne wypłaty:

$u_{1}(a)=-u_{2}(a),a\in A.$

Do takich gier można zaklasyfikować (pomijając remisy) gry towarzyskie (parlor games): szachy, GO, warcaby, klasyczne dwuosobowe gry karciane. ”Teoriogrowe” przykłady ściśle konkurencyjnych GS to: gra Kamień-Papier-Nożyczki, Orzeł-Reszka.

Skończone gry dwuosobowe o sumie zerowej nazywa się też grami macierzowymi.

Uwaga 5.1

Możemy sformułować równoważną definicję GS o sumie stałej używając strategii mieszanych: GS jest grą o sumie stałej jeżeli

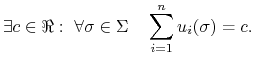$\exists c\in\Re:\ \forall\sigma\in\Sigma\quad\sum _{{i=1}}^{n}u_{i}(\sigma)=c.$

Równoważność wynika z liniowości funkcji wypłat względem poszczególnych argumentów profilu GS0.

Wszystkie poniższe definicje, o ile nie zostanie napisane inaczej, odnoszą sie do GS0.

Uwaga 5.2

Wypłaty w takich grach możeny zapisać w formie macierzowej:

$u_{1}(\sigma)=u_{1}(\sigma _{1},\sigma _{2})=\sigma _{1}A\sigma _{2}^{T},\ \ u_{2}(\sigma)=-u_{1}(\sigma)\quad\forall\sigma\in\Sigma,$

gdzie profil $\sigma _{1}$ jest wektorem wierszowym, $\sigma _{2}^{T}$ - wektorem kolumnowym.

Zdefiniujemy dwie liczby: $v_{1}$ : maximin, oraz $v_{2}$ : minimax.

Definicja 5.2

$v_{1}:=max_{{\sigma _{1}\in\Sigma _{1}}}min_{{\sigma _{2}\in\Sigma _{2}}}u_{1}(\sigma _{1},\sigma _{2})$

$v_{2}:=min_{{\sigma _{2}\in\Sigma _{2}}}max_{{\sigma _{1}\in\Sigma _{1}}}u_{1}(\sigma _{1},\sigma _{2}).$

$v_{1},\ v_{2}$ nazywamy też odpowiednio dolną i górna wartością GS0.

Uwaga 5.3

Gdy zastąpimy w tej definicji $\Sigma _{i}$ przez $A_{i}$ , czyli weźmiemy pod uwagę tylko strategie czyste, to w celu obliczenia $v_{1}$ bierzemy minimum z każdego wiersza macierzy wypłat gracza 1 i z tak uzyskanej kolumny znajdujemy maksimum.

Heurystycznie, maximin $v_{1}$ jest maksymalną wypłatą gracza 1 gdy gracz 2 minimalizuje wypłaty $u_{1}$ gracza 1. Dokładniej: dla każdego profilu $\sigma _{1}$ gracz 1 znajduje profil $\sigma _{2}$ który minimalizuje $u_{1}$ a ”następnie” 1 swoimi profilami $\sigma _{1}$ maksymalizuje $u_{1}$ . Otrzymana wartość $u_{1}$ to maximin; minimax $v_{2}$ jest wynikiem procedury optymalizacyjnej gracza 2, który wpierw maksymalizuje $u_{1}$ profilami $\sigma _{1}$ przy ustalonym $\sigma _{2}$ , a następnie minimalizuje $u_{1}$ swoimi profilami $\sigma _{2}$ .

Zauważmy że $v_{1},v_{2}$ można zdefiniować dla dowolnych (niekoniecznie o sumie zero) dwuosobowych GS.

Definicja 5.3

Profil $(\sigma _{1}^{*},\sigma _{2}^{*})$ jest punktem siodłowym jeżeli

$u_{1}(\sigma _{1},\sigma _{2}^{*})\le u_{1}(\sigma _{1}^{*},\sigma _{2}^{*})\le u_{1}(\sigma _{1}^{*},\sigma _{2})\ \ \forall\sigma _{i}\in\Sigma _{i},\ i=1,2.)$

Wypłatę $u_{1}(\sigma _{1}^{*},\sigma _{2}^{*})$ nazwiemy wartością gry (w punkcie siodłowym, saddle point value of the game).

Uwaga 5.4

Ponieważ

$-u_{1}(\sigma _{1}^{*},\sigma _{2}^{*})\ge-u_{1}(\sigma _{1}^{*},\sigma _{2}),$

więc, z uwagi na $u_{2}=-u_{1}$ , mamy

$u_{2}(\sigma _{1}^{*},\sigma _{2}^{*})\ge u_{2}(\sigma _{1}^{*},\sigma _{2}),$

a zatem punkt siodłowy GS0 jest RN GS0.

5.2. Własności. Podstawowe twierdzenia

Sformułujemy podstawowe twierdzenie dla rozważanych gier.

Twierdzenie 5.1 (”O minimaksie”, J. von Neumann, 1928)

Dla każdej 2-osobowej skończonej GS o sumie zerowej

1. Istnieje punkt siodłowy.

2. Istnieje $v^{*}\in\Re$ taka że $v_{1}=v_{2}=v^{*}$ , patrz Definicja 5.2.

3. Jeżeli $(\sigma _{1}^{*},\sigma _{2}^{*})$ jest punktem siodłowym to $u_{1}(\sigma _{1}^{*},\sigma _{2}^{*})=v^{*}$ .

4. $(\sigma _{1}^{*},\sigma _{2}^{*})$ jest punktem siodłowym wtedy i tylko wtedy gdy

$\sigma _{1}^{*}\in argmax_{{\sigma _{1}}}min_{{\sigma _{2}}}u_{1}(\sigma _{1},\sigma _{2})$

oraz

$\sigma _{2}^{*}\in argmin_{{\sigma _{2}}}max_{{\sigma _{1}}}u_{1}(\sigma _{1},\sigma _{2})$

Punkt 1 jest szczególnym ptzypadkiem Twieredzenia Nasha.

Punkt 2. mówi że w dwuosobowych GS0 maximin i minimaks są sobie równe.

Punkt 3. mówi że $v^{*}$ jest taka sama we wszystkich punktach siodłowych. W każdym punkcie siodłowym są jednocześnie spełnione najbardziej pesymistyczne przewidywania obu graczy. Gracz 1 otrzymuje wypłatę $u_{1}(\sigma _{1}^{*},\sigma _{2})=v^{*}$ , gracz 2 otrzymuje wypłatę $-u_{1}(\sigma _{1}^{*},\sigma _{2})=-v^{*}$ .

Punkt 4 mówi że w punkcie siodłowym gracz 1 gra strategią maximinową, gracz 2-i minimaksową.

1. Jest to szczególny przypadek twierdenia Nasha o istnieniu. Oryginalny dowód von Neumanna korzystał z innych technik matematycznych.

2. Wykażemy wpierw że $v_{2}\ge v_{1}$ . Niech $\sigma _{i}\in\Sigma _{i},i=1,2$ . Zachodzi

$min_{{\sigma _{2}^{{{}^{{\prime}}}}\in\Sigma _{2}}}u_{1}(\sigma _{1},\sigma _{2}^{{{}^{{\prime}}}})\le u_{1}(\sigma _{1},\sigma _{2}).$

(5.1)

Działając na powyższą nierówność operatorem $max_{{\sigma _{1}\in\Sigma _{1}}}$ otzymujemy

$v_{1}=max_{{\sigma _{1}\in\Sigma _{1}}}min_{{\sigma _{2}^{{{}^{{\prime}}}}\in\Sigma _{2}}}u_{1}(\sigma _{1},\sigma _{2}^{{{}^{{\prime}}}})\le max_{{\sigma _{1}\in\Sigma _{1}}}u_{1}(\sigma _{1},\sigma _{2}).$

(5.2)

Nierówność ta zachodzi dla każdego $\sigma _{2}\in\Sigma _{2}$ . Działając na powyższą nierówność operatorem $min_{{\sigma _{2}\in\Sigma _{2}}}$ otzymujemy

$v_{1}\le min_{{\sigma _{2}\in\Sigma _{2}}}max_{{\sigma _{1}\in\Sigma _{1}}}u_{1}(\sigma _{1},\sigma _{2})=v_{2}.$

(5.3)

co dowodzi nierowności $v_{2}\ge v_{1}$ .

Pokażemy teraz że $v_{1}\ge v_{2}$ . Wykorzystamy fakt istnienia RN. Niech $(\sigma _{1}^{*},\sigma _{2}^{*})$ będzie RN, czyli

$u_{1}(\sigma _{1}^{*},\sigma _{2}^{*})\ge u_{1}(\sigma _{1},\sigma _{2}^{*})\forall\sigma _{1}\in\Sigma _{1},$

(5.4)

oraz

$u_{1}(\sigma _{1}^{*},\sigma _{2}^{*})\le u_{1}(\sigma _{1}^{*},\sigma _{2})\forall\sigma _{1}\in\Sigma _{1}.$

(5.5)

Zachodzi też

$v_{1}=max_{{\sigma _{1}\in\Sigma _{1}}}min_{{\sigma _{2}\in\Sigma _{2}}}u_{1}(\sigma _{1},\sigma _{2})\ge min_{{\sigma _{2}\in\Sigma _{2}}}u_{1}(\sigma _{1}^{*},\sigma _{2}).$

(5.6)

Ponieważ, na mocy (5.5)

$min_{{\sigma _{2}\in\Sigma _{2}}}u_{1}(\sigma _{1}^{*},\sigma _{2})=u_{1}(\sigma _{1}^{*},\sigma _{2}^{*}),$

(5.7)

więc

$v_{1}\ge u_{1}(\sigma _{1}^{*},\sigma _{2}^{*}).$

(5.8)

Z uwagi na (5.4) mamy

$u_{1}(\sigma _{1}^{*},\sigma _{2}^{*})=max_{{\sigma _{1}\in\Sigma _{1}}}u_{1}(\sigma _{1},\sigma _{2}^{*})$

(5.9)

a więc

$v_{1}\ge max_{{\sigma _{1}\in\Sigma _{1}}}u_{1}(\sigma _{1},\sigma _{2}^{*})\ge min_{{\sigma _{2}\in\Sigma _{2}}}max_{{\sigma _{1}\in\Sigma _{1}}}u_{1}(\sigma _{1},\sigma _{2})=v_{2}.$

(5.10)

Wykazaliśmy $v_{1}\ge v_{2}$ i $v_{1}\le v_{2}$ , a zatem równość $v_{1}=v_{2}=v^{*}.$

3. Punkt 3 jest bezpośrednia konsekwencją powyższej równości. W każdej równowadze mamy więc:

Dla gracza 1:

$u_{1}(\sigma _{1}^{*},\sigma _{2}^{*})=max_{{\sigma _{1}\in\Sigma _{1}}}min_{{\sigma _{2}\in\Sigma _{2}}}u_{1}(\sigma _{1},\sigma _{2})=v^{*},$

(5.11)

a dla gracza 2

$u_{2}(\sigma _{1}^{*},\sigma _{2}^{*})=-min_{{\sigma _{2}\in\Sigma _{2}}}max_{{\sigma _{1}\in\Sigma _{1}}}u_{1}(\sigma _{1},\sigma _{2})=-v^{*}.$

(5.12)

Punkt 4 zostawiamy czytelnikowi jako ćwiczenie.

∎

Definicja 5.4

Liczbę $v^{*}$ nazywamy wartością (value) dwuosobowej GS o sumie zerowej.

Wartość ściśle konkurencyjnej GS0 jest to więc wypłata gracza 1 w punkcie siodłowym.

Definicja 5.5

Strategia $\sigma _{i}$ gracza $i$ rozwiązująca problem

$max_{{\sigma _{i}}}min_{{\sigma _{{-i}}}}u_{i}(\sigma _{i},\sigma _{{-i}}),\ \ i=1,2,$

nazywa sie strategią maksyminową gracza $i$ .

Twierdzenie 5.2

Jeżeli $v_{1}=v_{2}$ to (każdy) profil $(\sigma _{1}^{*},\sigma _{2}^{*})$ , gdzie $\sigma _{i}^{*}$ jest strategią maksyminową gracza $i,\ i=1,2$ jest punktem siodłowym.

Przykład 5.1

Znajdziemy strategię maksyminową i wypłatę ze strategii maksyminowej gracza 1 (wierszowego) w grze Orzeł – Reszka.

	B	S
B	1,-1	-1,1
S	-1,1	1,-1

Niech $\sigma _{1}=(p,1-p),\ \sigma _{2}=(y,1-y)$ . Obliczamy

$u_{1}(\sigma _{1},\sigma _{2})=(1-2p)(1-2y).$

Przy ustalonym $p$ : dla $p<1/2$ $u_{1}$ przyjmuje minimum dla $y=1$ , wynosi ono $2p-1<0$ . Dla $p=1/2$ minimum $u_{1}$ wynosi 0. Dla $p>1/2$ minimum $u_{1}$ jest dla $y=0$ i jest mniejsze od zera. Tak więc $max_{p}minu_{1}=0,$ strategia maksyminowa to profil $(1/2,1/2)$ z wypłatą 0. Analogicznie postępujemy dla gracza 2.

W każdej RN GS0 gracze otrzymują takie same (przeciwne co do znaku) wypłaty. Zachodzi też interesująca własność ”wymienności równowag” (equilibrium interchangeability). W 2-osobowych GS o sumie zerowej jeżeli gracz 1 wybierze swój profil z pewnej RN a drugi gracz wybierze swój z innej RN, to para tych profili też jest RN. Mówi o tym

Twierdzenie 5.3 (O wymienności równowag)

Niech $(a,b)\in\Sigma,\ (c,d)\in\Sigma$ - dwie RN dwuosobowej GS o sumie zerowej. Wtedy profile $(a,d),(c,b)$ też są RN.

Niech $v^{*}$ - wartość gry. W RN $(a,b)$ , ponieważ suma wypłat graczy jest zero oraz

$u_{2}(a,b)\ge u_{2}(a,\tilde{b})\ \forall\ \tilde{b}\in\Sigma _{2}$

(a zatem $-u_{2}(a,b)\le-u_{2}(a,\tilde{b})\ \forall\ \tilde{b}\in\Sigma _{2}$ ), więc otrzymujemy

$v^{*}=u_{1}(a,b)=-u_{2}(a,b)\le-u_{2}(a,\tilde{b})\ \forall\ \tilde{b}\in\Sigma _{2}.$

Podstawiając $\tilde{b}=d$ otrzymujemy obustronne oszacowanie

$v^{*}\le-u_{2}(a,d)=u_{1}(a,d)\le u_{1}(c,d)=v^{*},$

gdzie równość wynika z faktu że gra jest o sumie zerowej, a ostatnia nierówność z tego że $(c,d)$ jest RN. Wypłata $u_{1}(a,d)$ została obustronnie oszacowana przez $v^{*}$ , a zatem zachodzi równość $u_{1}(a,d)=v^{*}$ . Otrzymujemy

$u_{1}(a,d)=v^{*}=u_{1}(a,b)\ge u_{1}(\sigma _{1},d)\ \ \forall\sigma _{1}\in\Sigma _{1},$

gdzie nierówność z faktu że $(a,b)$ jest RN. Mamy też

$u_{1}(a,d)=u_{1}(a,b)=-u_{2}(a,b)\le-u_{2}(a,\sigma _{2})=u_{1}(a,\sigma _{2})\ \ \forall\sigma _{2}\in\Sigma _{2},$

nierówność wynika z faktu że $(a,b)$ jesr RN. Mnożąc przez $-1$ otrzymujemy stąd

$-u_{1}(a,d)\ge-u_{1}(a,\sigma _{2})\ \ \forall\sigma _{2}\in\Sigma _{2},$

a zatem

$u_{2}(a,d)=-u_{1}(a,d)\ge-u_{1}(a,\sigma _{2})=u_{2}(a,\sigma _{2})\ \ \forall\sigma _{2}\in\Sigma _{2}.$

Profil $(a,d)$ jest więc RN. Analogicznie dowodzimy że profil $(c,b)$ jest RN.

∎

Uwaga 5.5

Dla GS0 można podać efektywne algorytmy szukanie wartości gry za pomocą programowania liniowego, patrz np. monografia Luce, Reiffa [13].

Ćwiczenie 5.1

W symetrycznej GS0 $A_{1}=A_{2},\ u_{1}(a_{1},a_{2})=u_{2}(a_{2},a_{1})\ \forall a_{i}\in A_{i},i=1,2$ w mieszanej RN (jeżeli istnieje) zachodzi $u_{i}=0,\ i=1,2$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Teorii Gier