Zagadnienia

10.1 Równowaga Nasha (RN) w GE
10.2 Równowaga Doskonała
- 10.2.1 Metoda Indukcji Wstecznej (MIW)
10.3 Twierdzenia o istnieniu dla GE
10.4 GE z jednoczesnymi ruchami
10.5 GE z niedoskonałą informacją

10. Gry Ekstensywne II

10.1. Równowaga Nasha (RN) w GE

Definicja (ważna) 10.1

RN w $GE=\left\langle N,H,P,(\succeq _{i})_{{i\in N}}\right\rangle$ jest to profil

$s^{*}=(s_{1}^{*},s_{2}^{*},...,s_{n}^{*})$

taki że $\forall i\in N,\ \forall r_{i}\in S_{i}$ zachodzi

$u_{i}(O(s_{i}^{*},s_{{-i}}^{*}))\ge u_{i}(O(r_{i},s_{{-i}}^{*}))$

Uwaga 10.1

Gdy każdy gracz ma skończona liczbę strategii to RN znajdujemy biorąc wszystkie profile strategii, wyniki GE z profili i porównując wypłaty graczy na wynikach, tak jak w GS.

RN Gry Ekstensywnej (ze skończonymi zbiorami strategii graczy) jest to RN Postaci Strategicznej GE, czyli RN Gry Strategicznej: $<N,(S_{i})_{{i\in N}},(\bar{u}_{i})_{{i\in N}}>.$

Przykład 10.1

W Grze na Wejście (Przykład 9.3) RN to pary: (Enter, Agree), (Out, Fight).

Przykład 10.2

W grze Targ (Przykład 9.7) RN to pary $(C,EG),(D,FG),(C,EG).$

Przykład 10.3

W grze z Przykładu 9.8, RN to pary $(CH,F),(DG,E),(DH,E).$

Omówimy je w następnym rozdziale.

10.2. Równowaga Doskonała

Uwaga 10.2

Pełna nazwa: Równowaga doskonała za względu na podgry (Subgame Perfect Equilibrium, SPE).

Rozważmy Grę na Wejście. Oznaczamy: E – gracz 1-y (Entrant), M – 2-i (Monopolist), E=Enter, O=Out - strategie 1-go, A=Agree, F=Fight – 2-go. Są dwie RN postaci strategicznej: $(Out,Fight)$ i $(Enter,Agree)$ . Niech postać strategiczna tej GE ma macierz wypłat (”wartość monopolu” wynosi 6):

	Agree	Fight
Enter	3,3	-1,-1
Out	0,6	0,6

Rozważmy nastepujący scenariusz ”omyłki gracza 1”. Jest grana jedna z dwóch RN: Enter(Out,Fight) i (Enter, Agree). Gracz 1 zmienia omyłkowo strategię, gracz 2-i reaguje ”racjonalnie”: zmienia strategię tylko jeżeli podwyższy sobie wypłatę. Po ruchu gracza 2 gracz 1 reaguje ”racjonalnie” (już bez możliwości bez pomyłki). Zastosujmy ten scenariusz do obu RN.

$(Out,Fight)$ : 1 zmienia Out na Enter, wtedy 2 zmienia Fight na Agree, 1 pozostaje przy Agree. W efekcie $(Out,Fight)\rightarrow(Enter,Agree),$ czyli jedna równowaga przeszła w drugą.

$(Enter,Agree)$ : 1 zmienia Enter na Out, wtedy 2-i pozostaje przy strategii Agree, 1 wraca do Enter. W efekcie $(Enter,Agree)\rightarrow(Enter,Agree)$ , a zatem następuje powrót do RN (Enter,Agree).

Rozważmy analogiczny scenariusz ”omyłki gracza 2”. Daje on $(Out,Fight)\rightarrow(Enter,Agree),$ oraz $(Enter,Agree)\rightarrow(Out,Fight)$ .

Można powiedzieć że $(Out,Fight)$ jest ”mniej stabilna” ze względu na oba scenariusze łącznie, niż $(Enter,Agree)$ [trzy ”przejścia” dają $(Enter,Agree)$ , jedno $(Out,Fight)$ ]. W dalszej części wykładu pokażemy że równowagi różnią się też w aspekcie ”wiarygodności” (credibility): pierwsza z nich nie jest ”wiarygodna”.

Wprowadzimy pojęcie równowagi (Równowaga Doskonała ze względu na podgry) które eliminuje takie ”mniej niestabilne” równowagi. Wpierw zdefiniujemy podgry po niezakończonych historiach.

Definicja 10.2

$\forall h\in H\backslash Z$ podgra GE(h) po historii $h$ gry ekstensywnej $GE=\left\langle N,H,P,(\succeq _{i})_{{i\in N}}\right\rangle$

jest to następująca GE:

$GE(h):=\left\langle N,H^{{\prime}}(h),P^{{\prime}}_{h},(\gg)_{{i\in N}}\right\rangle,$

gdzie

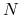$N$ jest to zbiór graczy, taki sam jak w wyjściowej GE
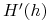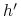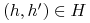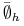
$H^{{\prime}}(h)$ jest to zbiór złożony z wszystkich ciagów $h^{{\prime}}$ akcji t. że $(h,h^{{\prime}})\in H$ , czyli że jest historią w wyjściowej GE, oraz z dodatkowego elementu który oznaczymy $\bar{\emptyset}_{h}$
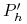$P^{{\prime}}_{h}$ –funkcja gracza:

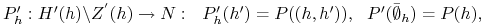$P^{{\prime}}_{h}:H^{{\prime}}(h)\backslash Z^{{{}^{{\prime}}}}(h)\rightarrow N:\ \ P^{{\prime}}_{h}(h^{{\prime}})=P((h,h^{{\prime}})),\ \ P^{{\prime}}(\bar{\emptyset}_{h})=P(h),$ gdzie

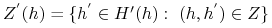
$Z^{{{}^{{\prime}}}}(h)=\{ h^{{{}^{{\prime}}}}\in H{{}^{{\prime}}}(h):\ (h,h^{{{}^{{\prime}}}})\in Z\}$
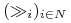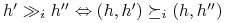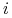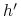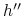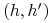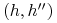$(\gg _{i})_{{i\in N}}$ preferencje graczy, t. że $h^{{\prime}}\gg _{i}h^{{\prime\prime}}\Leftrightarrow(h,h^{{\prime}})\succeq _{i}(h,h^{{\prime\prime}})$ , czyli gracz $i$ preferuje $h^{{\prime}}$ od $h^{{\prime\prime}}$ jeśli preferuje $(h,h^{{\prime}})$ od $(h,h^{{\prime\prime}})$ w wyjściowej GE.

Zachodzi $GE(\emptyset)=GE$ . Każdą inną podgrę nazywamy podgrą właściwą.

Każdej niezakończonej historii odpowiada 1 podgra (a więc liczba niezakończonych historii = liczba podgier).

Przykład 10.4

GE z Przykładu 9.7 ma 3 historie niezakończone: $\emptyset,(C),(D)$ , a wiec 3 podgry: $GE,GE((C))iGE((D))$ .

Przykład 10.5

GE z Przykładu 9.8 ma 3 historie niezakończone: $\emptyset,(C),(C,E)$ , a wiec 3 podgry: $GE,GE((C)),$ oraz $GE((C,E))$ .

Stosując powyższą terminologię wprowadzimy wpierw nieformalną definicję równowagi doskonałej GE.

Definicja 10.3 (nieformalna)

Równowaga doskonała (RD) w GE jest to profil strategii $(s_{1}^{*},...,s_{n}^{*})$ t. że $\forall i\in N,\ \forall$ podgry GE strategia $s_{i}^{*}$ jest optymalna w tej podgrze, tzn. jej zmiana nie podwyższa wypłaty gracza $i$ .

Przykład 10.6

W Grze na Wejście RN (Out, Fight) nie jest RD, gdyż w podgrze GE(Enter) strategia Fight gracza 2 nie jest optymalna - gracz 2 podwyższy swą wypłatę zmieniając ją na Agree. RN (Enter, Agree) jest RD: strategia każdego gracza jest optymalna zarówno w GE (=GE( $\emptyset$ )) jak i w GE(Enter).

Wprowadzimy notację potrzebną do formalnej definicji RD.

Niech $h\in H\backslash Z$ , $s$ - profil, $GE(h)$ - podgra po $h$ . Profil $s$ jednoznacznie wyznacza w podgrze $GE(h)$ pewną zakończoną historię $h^{{{}^{{\prime}}}}\in H^{{{}^{{\prime}}}}$ i w konsekwencji zakończoną historię $(h,h^{{{}^{{\prime}}}})$ w wyjściowej GE. Oznaczamy ją

$O_{h}(s)$

i nazywamy (zakończoną) historią po $h$ generowaną przez profil $s$ .

Tak więc $O_{h}(s)$ jest to zakończona historia w GE złożona z $h$ i z ciągu akcji generowanych przez profil $s$ po $h$ . W szczególności $O_{{\emptyset}}(s)=O(s)$ .

Przykład 10.7

W Grze na Wejście niech $s=(Out,Fight)$ , $h$ = $Enter$ . Mamy

$O_{h}(s)=(Enter,h^{{\prime}}):h^{{\prime}}$ to ciąg złożony z jednej akcji w GE(Enter), wyznaczony przez $s$ , czyli $h^{{\prime}}=Fight$ , a zatem $O_{h}(s)=(Enter,Fight).$

Definicja (ważna) 10.4

Profil $s^{*}=(s^{*}_{1},...,s^{*}_{n})$ jest Równowagą Doskonałą ze względu na podgry (w skrócie: RD) w GE (Subgame Perfect Equilibrium, SPE) jeśli

$\forall i\in N,\ \forall h\in H\backslash Z\$ takiej że $P(h)=i$ zachodzi

$u_{i}(O_{h}((s^{*}_{i},s^{*}_{{-i}})))\ge u_{i}(O_{h}((r_{i},s^{*}_{{-i}})))\quad\forall r_{i}\in S_{i}$

(mówimy: strategia $s^{*}_{i}$ jest optymalna w podgrze GE(h) ).

Zauważmy że w RD strategia każdego gracza ma być optymalna po każdej historii po której jest ruch tego gracza, podczas gdy w RN strategia każdego gracza ma być optymalna jedynie po historii $\emptyset$ . Ponieważ $O_{{\emptyset}}(s)=O(s)$ , więc każda RD jest RN. RD jest ulepszeniem, udoskonaleniem (refinement) RN. Znajdowaniu różnych udoskonaleń RN w GS i GE jest poświęcona bogata literatura, patrz np. [5, 10].

Uwaga 10.3

RD nie zawsze jest ”optymalnym” wyborem graczy. Przykład: eksperymenty laboratoryjne z grą w stonogę.

Przykład 10.8

W Grze na Wejście strategie 1-go to funkcje: $s_{1}:\{ h:P(h)=1\}\rightarrow A_{1}$ takie że

$s_{1}(h)\in A_{1}(h)=\{ a:(h,a)\in H\ \wedge\ P(h)=1\}.$

U nas

$h=\emptyset,\ \ \{ h:P(h)=1\}=\{\emptyset\},\ \ A_{1}(\emptyset)=\{ Enter,Out\},$

a zatem gracz 1 ma dwie strategie – odwzorowania $\{\emptyset\}\rightarrow\{ Enter,Out\},$

$\{ h:P(h)=2\}=\{ I\},\ A_{2}(Enter)=\{ Agree,Fight\},$

więc gracz 2 ma dwie strategie – odwzorowania $\{ Enter\}\rightarrow\{ Agree,Fight\}.$

Profil $s^{*}=(Out,Fight)$ nie jest RD, gdyż w podgrze GE(Enter) mamy:

$u_{2}(O_{{Enter}}(s^{*}))=u_{2}((Enter,Fight))=0,$

i zmiana strategii $Fight$ na $r_{2}=Agree$ daje graczowi 2 wypłatę

$u_{2}(O_{{Enter}}(Enter,Agree))=u_{2}(Enter,Agree)=2.$

Profil $s^{*}=(Enter,Agree)$ jest RD, gdyż

W $GE(\emptyset)$ profil $s^{*}$ jest RN, a więc zmiana strategii przez gracza 1 nie podwyższy jego wypłaty;

W GE(Enter) mamy $u_{2}(O_{{Enter}}(s^{*}))=u_{2}((Enter,Agree))=1,$ a zmiana strategii na $Fight$ daje graczowi 2 wypłatę $u_{2}(O_{{Enter}}(Enter,Fight))=u_{2}(Enter,Fight)=0.$

10.2.1. Metoda Indukcji Wstecznej (MIW)

Pod pojęciem rozwiązanie (wynik) GE chcielibyśmy rozumieć jej ”przebieg”, czyli informację, jakie akcje były grane przez graczy we wszystkich krokach GE. Ich znajomość daje nam zakończoną historię i odpowiadające jej wypłaty, czyli to co chvcielibyśmy rozumieć jako wynik gry. Dla pewnych typów GE rozwiązanie daje MIW. Jest to metoda znajdowania rozwiązania skończonych GE o skończonym horyzoncie i z doskonałą informacją (to ostatnie założenie można osłabić, odpowiednio modyfikując metodę). MIW polega na wyborze optymalnych akcji graczy w ich ostatnim ruchu i powtarzaniu tej procedury ”w tył” do początku gry. W kolejnych etapach MIW:

1. Znajdujemy optymalne akcje graczy wykonujących ruch w podgrach o długości 1 (długość podgry jest to długość najdłuższej historii w tej podgrze).

2. Powtarzamy to samo w podgrach o długości 2 itd., aż do wyjściowej GE.

3. Otrzymujemy w ten sposób pewną historię zakończoną którą nazwiemy wynikiem GE.

Przykład 10.11

W Grze na Wejście MIM daje RD (Enter, Agree). Gdy zmienimy wypłaty po akcji Fight gracza M z (0,0) na (0,1) to MIW nie można zastosować, bo w podgrze o długości 1 gracz M nie ma jednoznacznego wyboru. Są wtedy dwie RD: (Enter,Agree) oraz (Out,Fight).

Przykład 10.12

W GE Targ (Przykład 9.7) w podgrach o długości 1 jest ruch gracza 2: w GE(C) optymalna akcja 2 to E, w GE(D) - H. W podgrze o długości 2 jest ruch 1-go, jego optymalna akcja to C. RD = (C, EH). Historię $O((C,EH))=(C,E)\in Z$ łatwo uzyskujemy MIW.

Przykład 10.13

W GE z Przykładu 9.8 w podgrze GE((C,E)) o długości 1, tzn. po historii (C,E) gracz 1-y wybiera G. W podgrze GE(C) o długości 2, tzn po historii C, gracz 2-i wybiera E.W całej GE (o długości 3) gracz 1-y wybiera D. Tak więc RD=(DG,E). MIW daje D jako wynik gry, z wypłatami (2,0).

Podamy przykład GE z dwiema RD.

Przykład 10.14

Gracz 1-y ma akcje L, R. Po L 2-i może grać A z wypłatami (3,2), lub B, z wypłatami (0,0). Po R gracz 2-i może grać C z wypłatami (1,1), lub D z wypłatami (1,1).

RD: $(s_{1}^{*},s_{2}^{*})=(L,AC)$ oraz $(s_{1}^{*},s_{2}^{*})=(L,AD):$ wystarczy sprawdzić optymalność w podgrach GE(L), GE(R).

Dla RD $(s_{1}^{*},s_{2}^{*})=(L,AC)$ : W GE(h=L): $u_{2}(O_{h}(s_{1}^{*},s_{2}^{*}))=2\ge$ każda wypłata.

W GE(h=R): $u_{2}(O_{h}(s_{1}^{*},s_{2}^{*}))=u_{2}(R,C)=1\ge$ każdej wypłaty 2-go w GE(R).

Dla drugiej RD postępujemy analogicznie.

Tak samo pokazujemy że RN: $(R,BC),\ (R,BD)$ nie są RD. W tym przykładzie nie możemy zastosować MIW.

10.3. Twierdzenia o istnieniu dla GE

Przytoczymy podstawowe twierdzenia o RD.

Definicja 10.8

GE jest GE z doskonałą informacją jeżeli funkcja gracza jest jednowartościowa, każdy gracz zna wszystkie akcje grane do momentu w którym ma pojąć decyzję o wyborze akcji i zna wykonawców tych akcji.

Twierdzenie 10.2 (Kuhn)

Skończona GE z doskonałą informacją posiada RD. W skończonych GE z doskonałą informacją, w których gracze w każdym ruchu mają jednoznaczne preferencje wyboru akcji istnieje dokładnie jedna RD w strategiach czystych.

Uwaga 10.6

Twierdzenie nie zachodzi np. dla GE z nieskończoną liczbą historii, np. w trywialnej GE w której gracz wybiera liczbę z odcinka (0, 1) i otrzymuje wypłatę równą tej liczbie. Gracz nie ma strategii optymalnej, w szczegolności nie można zastosować MIW.

Jeżeli dla każdej podgry GE MIW wybiera optymalną akcję jednoznacznie, to uzyskany profil strategii jest jedyną RD GE (dowód pomijamy). Jeśli istnieje więcej niż jedna optymalna akcja, to pewna modyfikacja MIW daje wszystkie RD w skończonej GE.

10.4. GE z jednoczesnymi ruchami

Jeżeli w pewnym momencie GE decyzje podejmuje conajmniej dwóch graczy bez wiedzy jaką decyzję podjął każdy z tych graczy, to taką grę będziemy nazywać GE z Jednoczesnymi Ruchami (możemy bowiem wyobrażać sobie takią sytuację gdy gracze podejmują decyzje jednocześnie, w tej samej chwili). Będziemy używali skrótu GEzJR.

Przykład 10.22

n=3 graczy dzieli między siebie tort. Gracz 1 proponuje podział tortu na 3 części, gracze 2 i 3 bez wiedzy o swoich decyzjach (np. jednocześnie) wyrażają zgodę (T) lub nie (N). Jeśli 2 i 3 zagrają T, nastepuje podział, wpp. żaden z trzech graczy nic nie dostaje.

Formalna definicja GEzJR jest taka sama jak GE: GE z JR jest to czwórka

$GE=\left\langle N,H,P,(\succeq _{i})_{{i\in N}}\right\rangle$

w której $N,H,(\succeq _{i})_{{i\in N}}$ są takie same jak w GE, natomiast wartościami funkcji $P$ są zbiory graczy (podzbiory $N$ ) (podejmujących jednocześnie decyzje) a nie, jak w GE, pojedyńczy gracze.

Poza tym, o ile w GE historie są ciągami akcji, w GEzJR historie (poza pustą) to ciągi wektorów; współrzędne każdego wektora $a^{k}$ to ciągi akcji graczy podejmujących decyzje po historii $(a^{l})_{{l=1}}^{{l=k-1}}$ .

Formalizacja stategii, równowag, postaci strategicznej itp. w GEzJR jest podobna jak w przypadku GE i nie będziemy jej tu przedstawiać.

Uwaga 10.7

GS vs. GEzJR:

Dla każdej GS istnieje GEzJR w której każda historia zakończona $h\in Z$ ma długość 1, zbiór $Z$ jest zbiorem profili akcji w GS: $Z=\times A_{j},j\in N,\ P(\emptyset)=N,\ A_{j}(\emptyset)=A_{j}\ \ \forall j\in N.$

Uwaga 10.8

Każda skończona GE ma dokładnie jedną Postać Strategiczną. Odwrotnie nie, np.

	L	R
T	2,1	0,0
B	1,2	1,2

jest postacią strategiczną GEzJR, w której np. zbiór informacyjny gracza 2 jest dwuelementowy (także gracza 1–go), a także postacią strategiczną GE Na Wejście:

	Agree	Fight
Enter	2,1	0,0
Out	1,2	1,2

Uwaga 10.9

Każda skończona GE z doskonałą informacją ma RD w strategiach czystych. GEzJR nie musi mieć takiej RD. Przykładem może być GE w Orła i Reszkę, traktowana jako GEzJR, która nie ma RN (a więc i RD) w strategiach czystych.

10.5. GE z niedoskonałą informacją

Do tej pory zajmowaliśmy się GE z Doskonałą Informacją i używaliśmy skrótu GE. GE z Niedoskonałą Informacją (EG with Imperfect Information) definiujemy analogicznie, specyfikując dodatkowo informację jaką gracz posiada o dotychczasowym przebiegu gry gdy jest jego ruch. Niech $H_{i}$ oznacza zbiór historii po których jest ruch gracza $i$ . Określamy podział $H_{i}$ , jego elementy nazywamy zbiorami informacyjnymi. Historie $h,\ h^{{\prime}}$ należą do tego samego zbioru informacyjnego tylko wtedy gdy $A_{i}(h)=A_{i}(h^{{\prime}}),$ gdzie $A_{i}(h)$ – zbiór akcji gracza $i$ po $h$ .

W szczególności definicja ta dopuszcza ruchy określane jako losowe, ruchy Natury, po których zbiory informacyjne gracza który ma ruch po ruchu Natury nie są singletonami. Wtedy wynik gry jest to loteria na zbiorze zakończonych historii i preferencje graczy (utożsamiane u nas z wartościami oczekiwanymi wypłat) muszą być określane na tych loteriach.

Przykład 10.23

Prosty poker dwukartowy.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Teorii Gier