Zagadnienia

12.1 Wartość Shapley'a
12.2 Indeks siły Shapley'a–Shubika
12.3 Zbiory stabilne
12.4 Nukleous

12. Gry Koalicyjne II

12.1. Wartość Shapley'a

Uwaga 12.1

Ponieważ rdzeń może być pusty, ”nieintuicyjny”, lub np. składać się z continuum podziałów, więc należy szukać innej koncepcji ”rozwiązania” gry.

Dla GK $\left\langle N,v\right\rangle$ definiujemy

Definicja 12.1 (Wartość Shapley'a)

Wartość Shapley'a $\phi(v)$ GK $\left\langle N,v\right\rangle$ jest to wektor n liczb rzeczywistych

$\phi(v)=[\phi _{1}(v),...,\phi _{n}(v)]$

spełniających aksjomaty:

a1. Racjonalność grupowa (efektywność): $\sum _{{i\in N}}\phi _{i}(v)=v(N).$

Wektor wypłat $\phi(v)$ jest alokacją.

a2. Symetria: Jeżeli $v(S\cup\{ i\})=v(S\cup\{ j\})$ dla każdej koalicji $S:i\notin S,\ j\notin S$ , to $\phi _{i}(v)=\phi _{j}(v)$ .

Jeżeli $v$ jest symetryczna względem graczy $i,j$ to ich wartości Shapley'a (patrz 12.2) są jednakowe.

a3. Gracz nieistotny: Jeżeli $v(S)=v(S\cup\{ i\})$ dla każdej koalicji $S$ , to $\phi _{i}(v)=0$ .

Jeżeli gracz nie pomaga ani nie szkodzi żadnej koalicji to jego wartość Shapley'a jest zero.

a4. Addytywność: Jeżeli $u,v$ są funkcjami charakterystycznymi, to $\phi _{i}(u+v)=\phi _{i}(u)+\phi _{i}(v),\ i=1,...,n$ , gdzie $(u+v)(S):=u(S)+v(S)\ \forall S\subset N$ .

Jest to najsilniejsze założenie: wartość dwóch gier rozgrywanych ”łącznie” jest równa sumie wartości gier rozgrywanych ”oddzielnie” ( $u+v$ jest także funkcją charakterystyczną !).

Wartość Shapley'a jest imputacją. Daje ona ważny w zastosowaniach ”sprawiedliwy” podział wypłat wielkiej koalicji.

Definicja 12.2

Wartość Shapley'a gracza $i$ jest to współrzędna $\phi _{i}(v)$ wartości Shapley'a GK $<N,v>$ . opisuje wartość, siłę gracza w GK $<N,v>$ .

Twierdzenie (ważne) 12.1

Istnieje dokładnie jedna wartość Shapley'a GK $<N,v>$ .

Szkic dowodu: wpierw pokażemy że wartość Shapley'a $\phi(v)$ , jeżeli istnieje, jest dana wzorem:

$\phi _{i}(v)=\sum _{{S:i\in S}}{{c_{S}}/|S|},\ \ i=1,...,n,$

gdzie $c_{S}$ są JEDNOZNACZNIE wyznaczonymi stałymi. Następnie znajdziemy szczególną wartość Shapleya

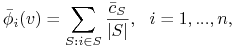$\bar{\phi}_{i}(v)=\sum _{{S:i\in S}}\frac{\bar{c}_{S}}{|S|},\ \ i=1,...,n,$

z explicite wyznaczonymi stałymi $\bar{c}_{S}$ . Ponieważ $c_{S}$ są jednoznaczne, więc $c_{S}=\bar{c}_{S}\ \forall S\subset N$ , a zatem $\phi _{i}(v)\equiv\bar{\phi}_{i}(v),\ i=1,...n$ , tzn. każda wartość Shapleya jest dana za pomoca powyższego wzoru, a więc jest dokładnie jedna. Wykażemy wpierw

Lemat 12.1

Wartość Shapley'a jest dana wzorem

$\phi _{i}(v)=\sum _{{i\in S}}\frac{c_{S}}{|S|},\ \ i=1,...,n,$

gdzie $c_{S}$ są wyznaczone JEDNOZNACZNIE wzorem rekurencyjnym (12.6) poniżej.

Rozważmy dowolną koalicję $\emptyset\neq S\subset N$ . Definiujemy funkcję charakterystyczną

$\displaystyle w_{S}(T)=\left\{\begin{array}[]{ll}1&jeżeli\ S\subset T\\ 0&wpp.\end{array}\right.$

(12.1)

Rozważamy GK $<N,w_{S}>$ (primitive game).

Fakt 1: W GK $<N,w_{S}>$ gracze spoza $S$ sa nieistotni:

$i\notin S\Rightarrow\phi _{i}(w_{S})=0$

Wykażemy, że

$\forall T\subset N:\ i\notin T\Rightarrow w_{S}(T)=w_{S}(T\cup\{ i\}).$

(12.2)

Na mocy aksjomatu a3, napisanego dla $S\rightarrow T$ i $v\rightarrow w_{S}$ będzie to oznaczało że $\phi _{i}(w_{S})=0$ .

Wzór (12.2) zachodzi gdyż:

Jeśli $T\supset S,$ to $w_{S}(T)=1$ , a więc tym bardziej $w_{S}(T\cup\{ i\})=1$ .

Jeśli $T\not\supset S,$ to są możliwe 3 przypadki:

$S\cap T=T,\ \ \ S\cap T=\emptyset,\ \ \ T\neq S\cap T\neq\emptyset.$

W każdym z nich $w_{S}(T)=0=w_{S}(T\cup\{ i\}),$ co dowodzi (12.2).

∎

Fakt 2: W GK $<N,w_{S}>$ ”gracze z $S$ są wymienialni” (interchangeable):

$i,j\in S\Rightarrow\phi _{i}(w_{S})=\phi _{j}(w_{S})$

Weźmy dowolną koalicję $T$ dla której $i\notin T,\ j\notin T$ . Dla tych $i,j$ stosujemy wzór (12.2): $w_{S}(T)=w_{S}(T\cup\{ i\})=w_{S}(T\cup\{ j\}).$ Z aksjomatu symetrii a2 otrzymujemy $\phi _{i}(w_{S})=\phi _{j}(w_{S})$ .

∎

Fakt 3: Dla GK $<N,w_{S}>$ zachodzi

$\sum _{{i\in N}}\phi _{i}(w_{S})=w_{S}(N)=1.$

Pierwsza równość to aksjomat a1, druga wynika z definicji $w_{S}$ .

∎

Fakt 4: Dla GK $<N,w_{S}>$ zachodzi

$\phi _{i}(w_{S})=\frac{1}{|S|}\ \ dla\ \ i\in S.$

$\sum _{{i\in N}}\phi _{i}(w_{S})=1=\sum _{{i\in S}}\phi _{i}(w_{S})+\sum _{{i\notin S}}\phi _{i}(w_{S})=|S|\phi _{i}(w_{S})+0.$ Pierwsza równość to Fakt 3, trzecia to Fakt 2 i Fakt 1. Dzieląc otrzymujemy tezę.

∎

Wniosek 12.1

$\displaystyle\phi _{i}(w_{S})=\left\{\begin{array}[]{ll}\frac{1}{|S|},&gdy\ \ i\in S\\ 0,&gdy\ \ i\notin S,\end{array}\right.$

(12.3)

gdzie $0$ wynika z Faktu 1.

Wniosek 12.2

$\displaystyle\phi _{i}(cw_{S})=\left\{\begin{array}[]{ll}\frac{c}{|S|},&gdy\ \ i\in S\\ 0,&gdy\ \ i\notin S,\end{array}\right.$

(12.4)

gdyż $cw_{S}$ też jest funkcją charakterystyczną.

Fakt 5: W dowolnej GK $<N,v>$ jej funkcję charakterystyczną $v$ można przedstawić w postaci

$v=\sum _{{S\subset N}}c_{S}w_{S},$

(12.5)

gdzie $c_{S}$ - JEDNOZNACZNIE wyznaczone stałe.

Definiujemy $c_{{\emptyset}}:=0$ , a dalsze stałe indukcyjnie (wpierw dla koalicji singlowych etc.):

$c_{S}:=v(S)-\sum _{{T\subset S,T\neq S}}c_{T}$

(12.6)

Dla każdej koalicji $S\subset N$ zachodzi

$\sum _{{T\subset N}}c_{T}w_{T}(S)=\sum _{{T\subset S}}c_{T}\cdot w_{T}(S)+\sum _{{T\not\subset S}}c_{T}\cdot w_{T}(S)=\sum _{{T\subset S}}c_{T}\cdot 1=\sum _{{T\subset S,T\neq S}}c_{T}+c_{S}=v(S),$

gdzie druga równość wynika z definicji $w_{T}$ ( $w_{T}=0$ dla $T\not\subset S$ , $w_{T}=1$ dla $T\subset S$ ), czwarta to definicja $c_{T}$ .

∎

Fakt 6: Dla GK $<N,v>$ wartość Shapley'a $\phi(v)=[\phi _{1}(v),...,\phi _{n}(v)]$ musi być postaci (jeśli istnieje)

$\phi _{i}(v)=\sum _{{S:i\in S}}\frac{c_{S}}{|S|},\ \ \ i=1,...,n.$

$\phi _{i}(v)=\phi _{i}(\sum _{{S}}c_{S}w_{S})=\sum _{{S}}\phi _{i}(c_{S}w_{S})=\sum _{{S:i\in S}}\phi _{i}(c_{S}w_{S})+\sum _{{S:i\notin S}}\phi _{i}(c_{S}w_{S})=\sum _{{S:i\in S}}\frac{c_{S}}{|S|}.$

Pierwsza równość wynika z Faktu 5, druga z aksjomatu a4, czwarta z Wniosku 12.2. Kończy to dowód Faktu 6, a więc i Lematu 12.1.

∎

Definicja 12.3

Wyrażenie $\Delta _{i}(S):=v(S)-v(S\backslash\{ i\})$ jest to wkład marginalny gracza $i$ do koalicji $S:i\in S$ .

Lemat 12.2

Wartość Shapley'a jest dana wzorem

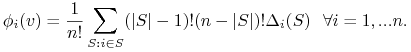$\phi _{i}(v)=\frac{1}{n!}\sum _{{S:i\in S}}(|S|-1)!(n-|S|)!\Delta _{i}(S)\ \ \forall i=1,...n.$

(12.7)

Sprawdzimy że $\phi(v)=[\phi _{1}(v),...,\phi _{n}(v)]$ jest wartością Shapley'a, tzn. spełnia aksjomaty a1-a4.

a4:

$\phi _{i}(u+v)=\sum\cdot\cdot\cdot[(u+v)(S)-(u+v)(S\backslash\{ i\})]=$

$=\sum\cdot\cdot\cdot[u(S)-u(S\backslash\{ i\})]+\sum\cdot\cdot\cdot[v(S)-v(S\backslash\{ i\})]=\phi _{i}(u)+\phi _{i}(v).$

a3: Mamy wykazać:

$\forall S\subset N:i\notin S\ \mbox{zachodzi implikacja}\ \ v(S)=v(S\cup\{ i\})\Rightarrow\phi _{i}(v)=0.$

Zdefiniujmy $T:=S\cup\{ i\}.$ Mamy z założenia $v(S)=v(S\cup\{ i\}),$ czyli $v(T\backslash\{ i\})=v(T)\ \forall T:i\in T.$ Tak więc dla każdej koalicji $T:i\in T\$ $i$ –ty składnik sumy we wzorze (12.7) jest równy 0.

a2: Mamy wykazać: Jeżeli $v(T\cup\{ i\})=v(T\cup\{ j\})$ dla każdej koalicji $T$ nie zawierającej $i,j$ , to $\phi _{i}(v)=\phi _{j}(v)$ .

Ustalmy gracza $i$ . We wzorze (12.7) sumowanie jest po wszystkich koalicjach $S$ dla których $i\in S.$ Dla takich $S$ zdefiniujmy $T:=S\backslash\{ i\}$ . Mamy $i\notin T$ , $|S|=|T|+1$ , oraz

$\phi _{i}(v)=\sum _{{S:i\in S}}|T|!(n-|T|-1)![v(T\cup\{ i\})-v(T)]=$

$=\sum _{{T:i\notin T}}|T|!(n-|T|-1)![v(T\cup\{ i\})-v(T)]=$

$=\sum _{{T\subset N}}|T|!(n-|T|-1)![v(T\cup\{ i\})-v(T)].$

Analogiczny wzór otrzymujemy dla $\phi _{j}(v)$ i korzystamy z założenia $v(T\cup\{ i\})=v(T\cup\{ j\})$ .

a1: Wynika z nastepującej interpretacji wzoru na $v(N)$ . Niech gracze dochodzą do wielkiej koalicji jeden po drugim. Rozważmy wszystkie możliwe sposoby czyli wszystkie permutacje $n$ graczy i załóżmy że każda zachodzi z jednakowym prawdopodobieństwem $1/n!$ . Wkład gracza $i$ do koalicji $S:i\in S$ wynosi $[v(S)-v(S\backslash\{ i\})]$ Przy każdej realizacji $\{ i_{1},...,i_{n}\}$ kolejności wchodzenia do wielkiej koalicji mamy [utożsamiamy $v(i)\equiv v(\{ i\})$ itp.]:

$v(N)=v(i_{1})+v(i_{1}\cup i_{2})-v(i_{1})+\cdot\cdot\cdot+v(N)-v(i_{1}\cup...\cup i_{{n-1}}).$

(12.9)

Niech $Z_{k}$ są zmiennymi losowymi (bo koalicje są tworzone losowo) których wartości

$Z_{{k}}:=v(i_{1}\cup...\cup i_{k})-v(i_{1}\cup...\cup i_{{k-1}}),\ \ k=2,...n,\ \ Z_{{1}}:=v(i_{1})$

dają wkład gracza wchodzącego do koalicji $\{ i_{1},...,i_{{k-1}}\}$ graczy.

Piszemy $n!$ razy wyrażenie na $v(N)$ , dla wszystkich permutacji graczy, czyli wszystkich sposobów formowania się wielkiej koalicji, sumujemy i dzielimy przez $n!$ . Lewa strona otrzymanego wyrażenia to $v(N)$ . Prawa strona jest równa $\sum _{{i\in N}}\phi _{i}(v).$ Tak więc $v(N)=\sum _{{i\in N}}\phi _{i}(v),$ co kończy dowód Lematu (12.2).

Przykładowo: dla $N=\{ 1,2,3\}$ :

$v(N)=v(i_{1})+v(i_{1}\cup i_{2})-v(i_{1})+v(N)-v(i_{1}\cup i_{2}).$

Piszemy odpowiednie wzory dla wszystkich permutacji $\{ 1,2,3\}$ :

$v(N)=v(1)+v(12)-v(1)+v(N)-v(12),$

$v(N)=v(1)+v(13)-v(1)+v(N)-v(13),$

$v(N)=v(2)+v(21)-v(2)+v(N)-v(21),$

$v(N)=v(2)+v(23)-v(2)+v(N)-v(23),$

$v(N)=v(3)+v(31)-v(3)+v(N)-v(31),$

$v(N)=v(3)+v(32)-v(3)+v(N)-v(32),$

i dodajemy, otrzymujemy tezę.

∎

Wcześniej pokazaliśmy (Fakt 6) że każda wartość Shapley'a (jeżeli istnieje) jest postaci

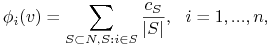$\phi _{i}(v)=\sum _{{S\subset N,S:i\in S}}\frac{c_{S}}{|S|},\ \ i=1,...,n,$

z jednoznacznie (indukcyjnie) wyznaczonymi stałymi $c_{S}$ . Wzór 12.7 także daje $c_{S}$ . Wartość Shapley'a jest więc wyznaczona jednoznacznie, co kończy dowód Twierdzenia.

∎

Uwaga 12.2

W dowodzie nie zakładaliśmy superaddytywności $v$ .

Uwaga 12.3

Każdą współrzędną wartości Shapley'a można wyrazić jako unormowaną sumę wkładów marginalnych: $\phi _{i}(v)=\frac{1}{n!}\sum _{{R}}\Delta _{i}(S_{i}(R)),$ gdzie sumujemy po wszystkich permutacjach $R$ zbioru N graczy, $S_{i}(R)$ oznacza zbiór graczy poprzedzających gracza $i$ w permutacji R wraz z graczem $i$ .

Wzór (12.7) ma nastepującą interpretację: $\phi _{i}(v)$ jest to wartość oczekiwana wkładu gracza $i$ do koalicji do której nie należy (do której dołącza), przy założeniu że wszystkie permutacje graczy w procesie formowania się wielkiej koalicji są jednakowo prawdopodobne (inaczej mówniąc, że proces formowania się wielkiej koalicji jest losowy).

Uwaga 12.4

Wartość Shapley'a superaddytywnej GK jest indywidualnie racjonalna. Wartość Shapley'a nie superaddytywnej GK nie musi być indywidualnie racjonalna, patrz Cwiczenie 12.15.

Relację między rdzeniem GK a jej wartością Shapley'a daje

Twierdzenie 12.2 (Ichiishi)

Jeśli GK z (niepustym) rdzeniem $C$ ma własność rosnących wkładów:

$\forall S,T,i:\quad(T\subset S,\ i\in T)\Rightarrow v(T)-v(T\backslash i)\le v(S)-v(S\backslash i)),$

to wartość Shapley'a $\phi\in C.$ Tak więc dla takich gier (por. gry wypukłe) rdzeń jest niepusty.

12.2. Indeks siły Shapley'a–Shubika

(Shapley–Shubik Power Index) Indeks siły Shapley'a–Shubika jest miarą siły graczy w ważnej klasie tzw. gier głosowania, w których proponoway kontrakt, decyzja, kandydat jest albo zaakceptowany albo odrzucony. Koalicje które są w stanie przegłosować dane propozycje są nazywane wygrywającymi, pozostale–przegrywającymi. Przyjmujemy że wartość zwycięskiej koalicji wynosi 1, przegrywającej 0.

Definicja 12.4

Gra Prosta (Simple Game). GK jest prosta jeżeli $\forall\ S\in 2^{N}\ v(S)\in\{ 0,1\}.$

W grach prostych jeżeli $v(S)=0$ to $S$ nazywa się koalicją przegrywającą, jeżeli $v(S)=1$ –wygrywającą.

Wniosek 12.4

W grach prostych dowolny podzbiór (nadzbiór) koalicji przegrywającej (wygrywającej) jest przegrywający (wygrywający).

Przykład 12.3

Gra na jednomyślność (The unanimity game)

$\displaystyle v(S)=\left\{\begin{array}[]{ll}1,&gdy\ \ S=N\\ 0,&wpp.\end{array}\right.$

(12.10)

Przykład 12.4 (Gra na większość)

$\displaystyle v(S)=\left\{\begin{array}[]{ll}1,&gdy\ \ |S|>n/2\\ 0,&wpp.\end{array}\right.$

(12.11)

Na przykład dla $n=3$ jedynie singletony i koalicja pusta są przegrywające.

Przykład 12.5

Gra głosowania ważonego (The weighted voting game)

$\displaystyle v(S)=\left\{\begin{array}[]{ll}1,&gdy\ \ \sum _{{i\in S}}w_{i}>q,\\ 0,&wpp.\end{array}\right.$

(12.12)

gdzie $w_{i},\ i=1,...n$ sa nieujemnymi wagami, $q>0$ (quota). Dla $q=(1/2)\sum _{{i\in N}}w_{i}$ grę nazywamy grą głosowania ważonego większościowego (the weighted majority voting game). Dla $w_{i}=\frac{1}{n}$ $q=\frac{1}{2}$ ; $v(S)=1\Leftrightarrow|S|>\frac{1}{2}$ .

Uwaga 12.5

Dla gier prostych wzór (12.7) upraszcza się, gdyż różnica $[v(S)-v(S\backslash\{ i\})]$ ma wartość 0 lub 1.

Definicja 12.6

Jeżeli $i\in S,\$ $v(S\backslash\{ i\})=0,$ oraz $v(S)=1$ to $i$ jest graczem krytycznym (critical player, swing voter) koalicji $S$ .

Licząc wartość Shapley'a gier prostych sumujemy w (12.7) jedynie po takich $S$ dla których gracz $i$ jest krytyczny. Otrzymujemy tzw. Indeks Siły Shapley'a–Shubika:

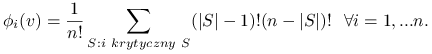$\phi _{{i}}(v)=\frac{1}{n!}\sum _{{S:i\ krytyczny\ S}}(|S|-1)!(n-|S|)!\ \ \forall i=1,...n.$

(12.13)

Indeks siły Shapleya-Shubika jest to wektor, którego współrzędne dają ułamek układów, w których dany głosujący (gracz) jest graczem krytycznym, czyli tym po przyłączeniu którego koalicja jest wygrywająca.

Przykład 12.6 (Gra prosta: głosowanie (patrz [36])A simple voting game)

$[6;4,3,2,1]$ : koalicja wygrywająca potrzebuje conajmniej 6 głosów, gracz A dostarcza 4 głosy, B 3, C 2, D 1 głos. Koalicje wygrywające to AB, AC, ABC, ABD, ACD, BCD, ABCD. A jest graczem krytycznym w 5 koalicjach, B i C w 3, D w jednej, więc indeks Banzhafa wynosi $5/12,3/12,3/12,1/12$ .

Przykład 12.7

Wartość Shapley'a dla gry Właściciel–Pracownicy dla $p=2$ pracowników

$\phi _{1}(v)=1/6[2!1!(f(2)-f(1))+1!1!f(1)]=1/6[2f(2)-f(1)].$

Przyjmujemy normalizację $f(2)=1,\ \ f(1)=\alpha\in[0,1]$ , otrzymując

$\phi _{1}=\phi _{2}=1/6(2-\alpha),\ \ \phi _{0}=f(2)-\phi _{1}-\phi _{2}=1/3(1+\alpha).$

Gdy drugi pracownik wnosi coraz mniejszy marginalny wkład do wielkiej koalicji, czyli dla $f(1)\longrightarrow f(2)$ , wartość Shapley'a właściciela: $\phi _{0}$ rośnie do $2/3$ .

Przykład 12.8

Wartość Shapley'a dla gry Rekawiczki dla n lewych i n+1 prawych rękawiczek wynosi:

Dla n=1: $(4/6,1/6,1/6)$ . Dla rosnacych n sumy wartości Shapley'a dla włascicieli lewych i prawych rękawiczek zbliżają się. Suma wartości Shapley'a dla $m=10^{6},n=10^{6}+1$ wynosi $0,500428$ dla właścicieli lewych rękawiczek, $0,499572$ dla prawych.

Oto następne przykłady pokazujące różnicę między wartością Shapley'a (indeksem siły Shapley'a–Shubika) a rdzeniem.

Przykład 12.9

Rynek z jednym sprzedawcą (1) i dwoma klientami (2,3).

$v(1,2,3)=v(1,3)=v(2,3)=1,v(S)=0$ dla pozostałych $S$ . $\phi(v)=(4/6,1/6,1/6),\ C=\{(1,0,0)\}$ .

Przykład 12.10

Gra ważonego głosowania: 4 graczy, wagi [2,1,1,1], suma wag = 5, wygrywa większość 3. Gracz 1 jest krytyczny gdy wchodzi do koalicji jako drugi lub trzeci. Pozostali gracze są symetryczni. Wartość Shapley'a to $(3/6,1/6,1/6,1/6)$ , rdzeń jest pusty. Gracz 1 ma $40\%$ głosów, ale jego wartość Shapley'a to połowa wartości wielkiej koalicji.

Przykład 12.11

Gra ważonego głosowania: 5 graczy, wagi [3,3,1,1,1].

Wartość Shapley'a to $(9/30,9/30,4/30,4/30,4/30)$ , rdzeń jest pusty. Tu proporcja jest odwrotna: Gracz 1 ma $33,33\%$ głosow, jego wartość to $(9/30\simeq 30\%$ wartości wielkiej koalicji.

Uwaga 12.6

Indeks siły Banzhafa (Banzhaf power index).

Istnieje szereg innych metod opisu siły graczy, wyborców. Jedną z najważniejszych jest Indeks Banzhafa. Indeks Banzhafa gracza jest wprost proporcjonalny do liczby koalicji, w których dany gracz jest wyborcą krytycznym, przy czym suma indeksów Banzhafa wszystkich graczy jest równa 1.

12.3. Zbiory stabilne

Zbiory stabilne zostały zaproponowane w monografii J. von Neumanna i O. Morgensterna [16] jako ”rozwiązanie” GK. Przystepne omówienie i przykłady mozna znależć np. w [36].

Definicja 12.7

W GK podział $x$ przebija podział $y$ jeżeli istnieje koalicja $S$ t. że

$\sum _{{i\in S}}x_{i}\le v(S)\ \ \mbox{oraz}\ \forall i\in S\ x_{i}>y_{i}.$

Uwaga 12.7

Rdzeń GK jest to zbiór jej podziałów nieprzebijalnych (przez żadne inne podziały).

Definicja 12.8

Zbiór $\Pi$ podziałów w GK jest zbiorem stabilnym tej GK jeżeli

1. $x\in\Pi,\ y\in\Pi\Rightarrow$ $x$ nie przebija $y$ .

2. $z\notin\Pi\Rightarrow\ \exists x\in\Pi:$ $x$ przebija $z$ .

Twierdzenie 12.3

[Dla danej GK z rdzeniem $C$ ]

1. Każdy zbiór stabilny zawiera $C$

2. Jeśli $C$ jest zbiorem stabilnym, to jest jedynym

3. Jeśli $A,B$ są zbiorami stabilnymi, to A nie jest podzbiorem właściwym B.

Gry na ogół mają wiele zbiorów stabilnych, mogą też (dla $n\ge 10$ ) ich nie mieć.

12.4. Nukleous

Nukleous został wprowadzony jako alternatywna koncepcja ”rozwiązania” GK. Przystepne omówienie i przykłady mozna znależć np. w [36]. W szczególności zachodzi

Twierdzenie 12.4

Nukleous jest jednoelementowy.

Jeśli rdzeń jest niepusty, to nukleous należy do rdzenia.

Przykład 12.15

$v(1)=v(2)=0,v(3)=1,v(\{ 1,2,3\}=5,\\ v(1,2)=3.5,v(1,3)=v(2,3)=0.$

Wartość Shapley'a $\phi(v)=(25/12,25/12,10/12)$ , a więc warunek indywidualnej racjonalności

$\phi _{i}(v)\ge v(\{ i\})$

nie jest spełniony dla $i=3$ . Koalicja $\{ 1,2\}$ nie spełnia warunku superaddytywności.

Ćwiczenie 12.2

Znależć wartość Shapley'a 3–osobowej GK Podział 1 $, w której koalicje 2 graczy mają wartość $\alpha\in[0,1]$ , jednoosobowe 0, wielka 1.

Rozwiązanie. Wstawiając do wzoru Shapley'a obliczamy $\phi _{i}=1/3,\ i=1,2,3.$ Można też zgadnąć z symetrii graczy.

Ćwiczenie 12.3

Znaleźć wartości Shapleya dla Gry Bankructwo 11.5, 11.6, 11.7.

Odp. $\phi=(7,12,17),\ (6,11,19),\ (11,11,14).$

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Teorii Gier