Zagadnienia

2.1 Gra strategiczna
2.2 Równowaga Nasha w strategiach czystych
2.3 Strategie mieszane
2.4 Dominacje strategii

2. Gry w postaci strategicznej

2.1. Gra strategiczna

Wprowadzamy oznaczenia

$N=\{ 1,2,...n\}-\mbox{zbiór graczy}$

$A_{i},i=1,2,...n-\mbox{niepusty zbiór akcji (strategii czystych) gracza}\ i$

$A=\times A_{i},i\in N$ .

$u_{i}:A\rightarrow\Re-\mbox{wypłata (funkcja wypłat) gracza}\ i,\ i=1,...n$

Definicja (ważna) 2.1

Gra strategiczna jest to trójka $GS=\left\langle N,(A_{i})_{{i\in N}},(u_{i})_{{i\in N}}\right\rangle$

Używa się też terminów: gra w postaci strategicznej, gra w postaci normalnej, gra niekooperacyjna.

Oznaczamy

$a=(a_{1},a_{2},...a_{n})=(a_{i})_{{i\in N}}-\mbox{profil (strategii czystych) gry},\ a_{i}\in A_{i}.$

$u_{i}(a)-\mbox{wypłata gracza $i$ z profilu $a$}$

Niekiedy, chcąc wyróżnić gracza $i$ , np. by porównywać wartości funkcji wypłat w profilach w których zmieniamy jedną współrzędna, będziemy profil zapisywali w postaci $(a_{i},a_{{-i}})$ , gdzie $a_{{-i}}$ oznacza ciąg wyrazów profilu $(a_{j})$ dla wszystkich graczy poza $i$ : $a_{{-i}}=(a_{j})_{{j\in N\backslash\{ i\}}}$ . Konsekwentnie oznaczamy $A_{{-i}}=\times A_{k},\ k\in N\backslash\{ i\}$

Uwaga 2.1

Tam gdzie nie będzie wątpliwości, będziemy utożsamiać akcję ze strategią. W ogólności, dla wielu typów gier strategia to scenariusz, plan działań, akcji na wszystkie możliwe sytuacje. Odpowiednie formalne definicje będą podane w dalszych rozdziałach.

Uwaga 2.2

Ogólniejsza definicja gry strategicznej wprowadza pojęcie wynikow gry i zastepuje funkcje wypłat graczy przez relacje preferencji na zbiorze wyników gry. W tym wykładzie relacje preferencji specyfikujemy przez podanie funkcji użyteczności - funkcji wypłat, które te relacje określają. Więcej na ten temat - patrz np. [13, 16, 20, 14].

Przykład 2.1

$N=\{ 1,2\}$ , $A_{1}=\{ 1,2,...m_{1}\},\ A_{2}=\{ 1,2,...m_{2}\}$ . Niech $a=(a_{1},a_{2})\in A=A_{1}\times A_{2}$ - profil strategii czystych, $u_{i}(a)$ - wyplata gracza $i$ z profilu $a$ , $i=1,2.$ W ogólności zbiory $A_{i}$ mogą być zbiorami różnych strategii. Zbiory $\{ u_{i}(a),a\in A\}$ mają po $m_{1}\times m_{2}$ elementów, które tworzą ${m_{1}\times m_{2}}$ elementowe macierze - macierze wypłat graczy. Niech $E$ oznacza macierz wypłat gracza 1, $F$ –gracza 2:

$E=(e_{{hk}}),\ e_{{hk}}=u_{1}(h,k),\ F=(f_{{hk}}),\ f_{{hk}}=u_{2}(h,k)\ \forall h\in A_{1},\forall k\in A_{2}.$

Numer wiersza odpowiada numerowi strategii gracza 1, numer kolumny - numerowi strategii gracza 2.

Przykład 2.2

Jako szczególny przypadek Przykładu 2.1 przyjmijmy

$N=\{ 1,2\},\quad A_{1}=A_{2}=\{ C,D\},$ oraz

$u_{1}((C,C))=R,\ u_{1}((C,D))=S,\ u_{1}((D,C))=T,\ u_{1}((D,D))=P$ ,

$u_{2}((C,C))=R,\ u_{2}((C,D))=T,\ u_{2}((D,C))=S,\ u_{2}((D,D))=P,\ T,R,P,S\in\Re.$ Macierze $E,F$ wypłat gracza 1 i 2 mają postać odpowiednio

E	C	D
C	R	S
D	T	P

F	C	D
C	R	T
D	S	P

Będziemy używać łącznego zapisu

	C	D
C	R,R	S,T
D	T,S	P,P

W szczególoności dla $T>R>P>S$ otrzymujemy Dylemat Więźnia, z oznaczeniami: C = Cooperation, D = Defection.

2.2. Równowaga Nasha w strategiach czystych

Definicja (ważna) 2.2

Równowaga Nasha w strategiach czystych (RN) gry strategicznej

$GS=\left\langle N,(A_{i})_{{i\in N}},(u_{i})_{{i\in N}}\right\rangle$

jest to profil akcji (strategii czystych) $a^{*}=(a^{*}_{1},a^{*}_{2},...,a^{*}_{N})\in A$ t. że $\forall i\in N\ \forall a_{i}\in A_{i}$

$u_{i}(a^{*}_{i},a^{*}_{{-i}})\ge u_{i}(a_{i},a^{*}_{{-i}})$

Okazuje się że wiele gier nie ma RN w strategiach czystych, np. gra Orzeł - Reszka z Przykładu 1.4.

2.3. Strategie mieszane

Rozważmy grę ”W Kotka i Myszkę” z Przykładu 1.5, o macierzy wypłat

	L	P
L	0,2	1,0
P	1,0	0,2

gdzie myszka (M) jest graczem wierszowym, kot (K) - graczem kolumnowym i nie ma RN w strategiach czystych.

Rozważmy intuicyjny sposób wprowadzenia strategii mieszanych. Niech M wybiera akcję L z prawdopodobieństwem $x$ , P z $1-x$ , K wybiera L z p-stwem $y$ , P z $1-y$ . Nazwijmy pary $(x,1-x),\ (y,1-y)$ strategiami mieszanymi odpowiednio M i K. Można pokazać że para strategii $((1/2,1/2),(1/2,1/2))$ ma tę własność że oczekiwana wartość wypłaty M (K) nie podniesie się (w istocie–nie ulegnie zmianie, co będzie wynikało z ogólnej teorii przedstawionej w następnej części) jeżeli dowolnie zmienimy $x(y)$ (patrz Ćwiczenie 3.2, Ćwiczenie 3.3 ).

Można więc nazwać tę parę równowagą Nasha dla strategii mieszanych.

Definicja 2.3

GS jest skończona jeżeli $m_{i}\equiv|A_{i}|<\infty,i=1,2,...n$ .

W dalszym ciągu, o ile nie będzie to powiedziane explicite inaczej, będziemy rozważać gry skończone. Definiujemy

Definicja 2.4

Strategia mieszana $\sigma _{i}$ gracza $i$ w grze strategiczej $GS=\left\langle N,(A_{i})_{{i\in N}},(u_{i})_{{i\in N}}\right\rangle$ jest to rozkład prawdopodobieństwa na zbiorze jego strategii czystych $A_{i}$ :

$\sigma _{i}=(\sigma _{{i1}},\sigma _{{i2}},...,\sigma _{{im_{i}}})$

Współrzędna $\sigma _{{ih}}\ge 0$ jest prawdopodobieństwem że gracz $i$ zagra strategią czystą (wybierze akcję) $h\in A_{i}$ . Wprowadzamy oznaczenia:

$\Sigma _{i}=\{\sigma _{i}:A_{i}\rightarrow[0,1]:\sum _{{k=1}}^{{m_{i}}}\sigma _{{ik}}=1,\ \sigma _{{ik}}\ge 0\}$ – zbiór strategii mieszanych gracza $i$

$\sigma\equiv(\sigma _{j})_{{j\in N}}=(\sigma _{1},\sigma _{2},...\sigma _{n})-\mbox{profil gry}$

$\Sigma=\times\Sigma _{i},\ i\in N$ – zbiór wszystkich profili gry

$\sigma _{{-i}}=(\sigma _{1},\sigma _{2},..\check{\sigma}_{i}.,.,\sigma _{N})$ - profil strategii wszystkich graczy poza graczem $i$ .

$u_{i}(\sigma)=u_{i}(\sigma _{i},\sigma _{{-i}})-\mbox{wypłata gracza $i$ z profilu $\sigma$}$

W dalszym ciągu zamiast strategia mieszana będziemy mówić strategia. Strategia czysta jest szczególnym przypadkiem strategii mieszanej; czasami gdy będziemy chcieli podkreślić że mamy do czynienia ze strategią czystą będziemy zamiast strategia mówić strategia czysta.

Strategie mieszane opisują sytuacje w których gracze podejmują akcje z pewnym prawdopodobieństwem. Można sobie wyobrażać że każdy gracz posiada urządzenie dające rozkład p-stwa określający jego strategię mieszaną i używaja tego urządzenia do gry. Alternatywna interpretacja strategii mieszanych jest następująca. Każdemu graczowi odpowiada jedna ”bardzo duża” populacja graczy. Częstość występowania w niej graczy grających każdą z akcji ze zbioru $A_{i}$ jest równa p-stwu występowania tej akcji w strategii mieszanej. Gracz $i$ losuje z tej populacji jednego gracza i gra jego strategią.

Każda strategia mieszana $\sigma _{i}$ każdego gracza $i$ jest opisana przez wektor pewien wektor $x_{i}=(x_{{i1}},...,x_{{im_{{i}}}})$ w przestrzeni euklidesowej $R^{{m_{{i}}}}.$ Będziemy używać alternatywnie zapisu: $\sigma _{i}=(\sigma _{{i1}},...,\sigma _{{im_{{i}}}})$ oraz, gdy będziemy chcieli podkreślić algebraiczną strukture wprowadzanego formalizmu, powyższej reprezentacji $x_{i}$ . Profil $\sigma$ gry będziemy alternatywnie oznaczać przex $x$ , $x=(x_{1},...x_{N}).$ Z definicji rozkładu p-stwa mamy

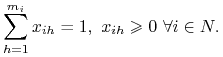$\sum _{{h=1}}^{{m_{i}}}x_{{ih}}=1,\ x_{{ih}}\ge 0\ \forall i\in N.$

Współrzędna $x_{{ih}}$ jest prawdopodobieństwem że gracz $i$ zagra strategią czystą (wybierze akcję) $h\in A_{i}$ .

Definicja 2.5

Niech $\forall i\in N\ A_{i}=A$ , czyli zbiór akcji jest ten sam dla wszystkich graczy. GS jest symetryczna $\Leftrightarrow\forall i\ne j,\ \forall a=(a_{1},...a_{n})$ zachodzi

$u_{j}(a_{1},...,a_{i},...a_{j},...a_{n})=u_{i}(a_{1},...,a_{j},...,a_{i},...,a_{n}).$

Mówimy że GS jest symetryczna jeżeli wypłaty każdych dwóch graczy nie ulegają zmianie przy zamianie ról tych graczy.

Uwaga 2.3

Dla n=2 i gry symetrycznej $u_{2}(a_{1},a_{2})=u_{1}(a_{2},a_{1})$ , macierze wypłat graczy są transponowane. Ogólniej, dla n=2 symetria sprowadza sie do stwierdzenia że macierze wypłat są kwadratowe i jedna powstaje z drugiej przez transpozycję.

Wypłaty graczy z profili strategii mieszanych.

Dla każdego gracza $i$ definiujemy $\Delta _{i}$ - sympleks jednostkowy gracza $i$ (sympleks strategii mieszanych gracza $i$ ) oraz $\Delta$ - sympleks strategii mieszanych GS:

Definicja 2.6

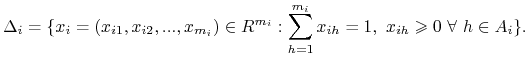$\Delta _{i}=\{ x_{i}=(x_{{i1}},x_{{i2}},...,x_{{m_{i}}})\in R^{{m_{i}}}:\sum _{{h=1}}^{{m_{i}}}x_{{ih}}=1,\ x_{{ih}}\ge 0\ \forall\ h\in A_{i}\}.$

$\Delta=\times _{{i}}\Delta _{i}.$

Tak więc elementy sympleksu jednostkowego gracza utożsamiamy z jego strategiami mieszanymi. Zbiory $\Delta _{i},\ i=1,...n,\ \Delta$ są zwarte i wypukłe, co bedzie w szczegolności odgrywało rolę w dowodzie istnienia równowagi Nasha.

Przykład 2.3

$\$ Dla $N=\{ 1,2\},\ m_{1}=m_{2}=2,\ x_{1}=(x_{{11}},x_{{12}}),\ x_{2}=(x_{{21}},x_{{22}}),$ sympleksy obu graczy są odcinkami o długości $\sqrt{2}$ . Dla $N=\{ 1,2\},\ m_{1}=m_{2}=3$ sympleksy obu graczy są trójkątami równobocznymi.

Strategia czysta jest szczególnym przypadkiem strategii mieszanej. Oznaczając

$e_{i}^{k}=(0,...0,1,0,...0)$

(2.1)

- $k$ -ty wersor w $\Re^{{m_{i}}}$ , możemy zapisać wektorową reprezentację profilu $x_{i}=(x_{{i1}},...,x_{{im_{i}}})$ w nastepujący sposób:

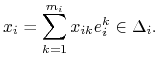$x_{i}=\sum _{{k=1}}^{{m_{i}}}x_{{ik}}e_{i}^{k}\in\Delta _{i}.$

(2.2)

Można powiedzieć że wektor $e_{i}^{k}$ jest strategią (mieszaną) gracza $i$ przypisującą akcji o numerze $k$ ze zbioru $A_{i}$ prawdopodobieństwo 1, $e_{i}^{k}$ jest $k$ -tą strategią czystą gracza $i$ . Dla każdego gracza $i$ wierzchołki sympleksu $\Delta _{i}$ są to elementy bazy kanonicznej $\{ e_{i}^{1},...,e_{i}^{{m_{i}}}\}$ przestrzeni wektorowej $R^{{m_{i}}}$ .

Rozważmy $GS=\left\langle N,(A_{i})_{{i\in N}},(u_{i})_{{i\in N}}\right\rangle$ . Założenie że każdy gracz podejmuje decyzję o wyborze akcji ”niezależnie”, bez wiedzy o wyborze innych graczy, formalizujemy w postaci tzw. postulatu niezależności stochastycznej.

Definicja 2.7

Niech $a=(a_{1},...a_{n}),\ a_{i}\in A_{i}$ - profil strategii czystych GS. Postulat niezależności statystycznej mówi że (łączne) p-stwo że 1-y gracz wybierze akcję (zagra) $a_{1}$ , …, $n$ -ty zagra $a_{n}$ jest dane wyrażeniem

$x(a)=x_{{1a_{1}}}x_{{2a_{2}}}...x_{{na_{n}}}$

gdzie $x_{{ia_{i}}}$ jest p-stwem że gracz $i$ zagra $a_{i},\ i=1,...n$ .

W ten sposób każdemu profilowi strategii czystych $a\in A$ gry GS przyporządkowaliśmy liczbę $x(a)\ge 0$ . Zachodzi przy tym

$\sum _{{a\in A}}x(a)=1$

(2.3)

Dla każdego gracza $i$ procedura ta definiuje na zbiorze $A=\times A_{i},\ i=1,...n$ profili strategii czystych gry pewną zmienna losową $U_{i}$ o rozkładzie

$(u_{i}(a),x(a)),\ a\in A$

(2.4)

gdzie $u_{i}(a)$ jest wypłatą gracza $i$ z profilu $a$ , natomiast $x(a)$ jest zdefiniowanym wyżej prawdopodobieństwem zagrania tego profilu.

Definicja 2.8

Wypłata gracza $i$ z profilu strategii mieszanych $x=(x_{1},...x_{n})$ jest to wartość oczekiwana zmiennej losowej $U_{i}$ :

$\tilde{u}_{i}(x)=\sum _{{a\in A}}u_{i}(a)x(a)$

W dalszym ciagu będziemy na ogół zastępować $\tilde{u}_{i}(x)$ przez $u_{i}(x)$ , oraz pomijać jedną parę nawiasów tam gdzie nie budzi to wątpliwości. Np. zamiast $u_{i}((x_{1},x_{2}))$ będziemy pisać $u_{i}(x_{1},x_{2}).$

Funkcje wypłat są liniowe względem poszczególnych współrzędnych profilu gry (w dalszym ciagu będziemy używali zwrotu: wypłaty są liniowe). Mówi o tym

Stwierdzenie 2.1

O liniowości wypłat względem każdej współrzednej pofilu

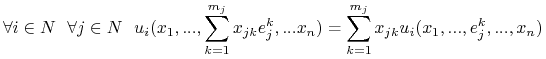$\forall i\in N\ \ \forall j\in N\ \ u_{i}(x_{1},...,\sum _{{k=1}}^{{m_{{j}}}}x_{{jk}}e_{j}^{k},...x_{{n}})=\sum _{{k=1}}^{{m_{{j}}}}x_{{jk}}u_{i}(x_{1},...,e_{j}^{k},...,x_{{n}})$

(2.5)

Wykorzystując postulat niezależności statystycznej [ $x(a)=x_{{1a_{1}}}...x_{{ja_{j}}}...x_{{na_{n}}}$ ] prawą stronę przepisujemy w postaci

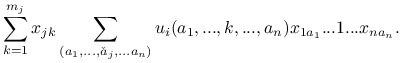$\sum _{{k=1}}^{{m_{{j}}}}x_{{jk}}\sum _{{(a_{1},...,\check{a}_{j},...a_{n})}}u_{i}(a_{1},...,k,...,a_{n})x_{{1a_{1}}}...1...x_{{na_{n}}}.$

Lewa strona ma postać

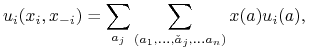$u_{i}(x_{i},x_{{-i}})=\sum _{{a_{j}}}\sum _{{(a_{1},...,\check{a}_{j},...a_{n})}}x(a)u_{i}(a),$

Wyciągając $x_{{ja_{j}}}$ z $x(a)$ przed ”wewnętrzną” sumę i pamiętając że $\sum _{{a_{j}\in A_{j}}}x_{{ja_{j}}}=\sum _{{k=1}}^{{m_{{j}}}}x_{{jk}}$ otrzymujemy tezę.

∎

W szczególności dla $j=i$ otrzymujemy wykorzystywana w dalszych rozważaniach równość

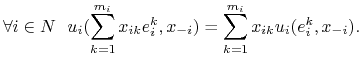$\forall i\in N\ \ u_{i}(\sum _{{k=1}}^{{m_{{i}}}}x_{{ik}}e_{i}^{k},x_{{-i}})=\sum _{{k=1}}^{{m_{{i}}}}x_{{ik}}u_{i}(e_{i}^{k},x_{{-i}}).$

Przykład 2.4

N=2. Oznaczmy $A,B$ - macierze wypłat odpowiednio gracza 1,2. Wypłata gracza 1 z profilu $x=(x_{1},x_{2})$ :

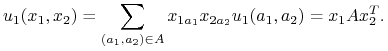$u_{1}(x_{1},x_{2})=\sum _{{(a_{1},a_{2})\in A}}x_{{1a_{1}}}x_{{2a_{2}}}u_{1}(a_{1},a_{2})=x_{1}Ax_{2}^{T}.$

Analogicznie dla drugiego gracza $u_{2}(x_{1},x_{2})=x_{1}Bx_{2}^{T}.$ W szczególności dla gry symetrycznej, tzn. gdy $u_{1}(x_{1},x_{2})=u_{2}(x_{2},x_{1})$ , czyli $A=B^{T}$ .

Uwaga: $(x_{i},x_{{-i}})$ oznacza profil $(x_{1},x_{2},...x_{n})$ , a nie profil $(x_{i},x_{1},...\check{x}_{i},...,x_{n})$ . W szczególności, dla $n=2,i=2$ mamy $x_{{-i}}=x_{1}$ , ale formalny zapis $u_{i}(x_{i},x_{{-i}})\equiv u_{2}(x_{2},x_{1})$ jest to wartość funkcji wypłat $u_{2}$ na profilu (w punkcie) $(x_{1},x_{2}),$ a nie na $(x_{2},x_{1}).$

Definicja 2.9

Rozszerzenie mieszane skończonej gry strategicznej $GS\ \left\langle N,(A_{i})_{{i\in N}},(u_{i})_{{i\in N}}\right\rangle$ jest to trójka

$\tilde{GS}=\left\langle N,(\Sigma _{i})_{{i\in N}},(\tilde{u}_{i})_{{i\in N}}\right\rangle.$

W dalszym ciągu rozszerzenie mieszane także oznaczamy skrótem $GS$ .

2.4. Dominacje strategii

Definicja 2.10

Strategia $\sigma _{i}\in\Sigma _{i}$ ściśle dominuje strategię $\eta _{i}\in\Sigma _{i}$ jeżeli

$\forall\ \sigma _{{-i}}\in\Sigma _{{-i}}\ \ \ u_{i}(\sigma _{i},\sigma _{{-i}})>u_{i}(\eta _{i},\sigma _{{-i}})$

Definicja 2.12

Strategia $\sigma _{i}\in\Sigma _{i}$ słabo dominuje strategię $\eta _{i}\in\Sigma _{i}$ jeżeli

$\forall\ \sigma _{{-i}}\in\Sigma _{{-i}}\ \ \ u_{i}(\sigma _{i},\sigma _{{-i}})\ge u_{i}(\eta _{i},\sigma _{{-i}})$

oraz istnieje podprofil $\sigma _{{-i}}\in\Sigma _{{-i}}$ dla którego powyższa nierówność jest ostra.

Mówimy że odpowiednie strategie $\eta _{i}$ sa ściśle (słabo) zdominowane przez powyższe strategie $\sigma _{i}$ . Strategia jest słabo zdominowana jeżeli istnieje inna która ją słabo dominuje.

Przykład 2.5

W DW (czysta) strategia D (i.e. $\sigma _{i}=(0,1),\ i=1,2$ ) ściśle dominuje każdą inną strategię gracza $i$ .

Przykład 2.6

W Słabym DW

	C	D
C	R,R	S,T
D	T,S	S,S

$T>R>S,$ strategia $D$ nie dominuje ściśle strategii $C$ gracza. Mamy bowiem np. dla $i=1$ –ego gracza, oznaczając $\sigma _{2}=(\beta,1-\beta)$ :

$u_{1}(D,\sigma _{2})=\beta T+(1-\beta)S,$

$u_{1}(C,\sigma _{2})=\beta R+(1-\beta)S,$

a zatem dla $\beta=0,$ czyli dla $\sigma _{2}=(0,1)$ , zachodzi równość $u_{1}(D,\sigma _{2})=u_{1}(C,\sigma _{2})$ .

Przykład 2.7

W Słabym DW (czysta) strategia $\sigma _{1}=D$ słabo dominuje strategię $\eta _{1}=C$ 1–go gracza. Mamy bowiem, dla $i=1,$ $\ \sigma _{{-i}}\equiv\sigma _{2}:=(\beta,1-\beta),$ z liniowości,

$u_{1}(D,\sigma _{2})\ge u_{1}(C,\sigma _{2}),$

oraz $\forall\sigma _{2}\neq(1,0)$ :

$u_{1}(D,\sigma _{2})>u_{1}(C,\sigma _{2})$

Uwaga 2.4

Scisła dominacja implikuje słabą dominację.

Definicja 2.13

Strategia $\sigma _{i}\in\Sigma _{i}$ dominuje strategię $\eta _{i}\in\Sigma _{i}$ jeżeli

$\forall\ \sigma _{{-i}}\in\Sigma _{{-i}}\ \ \ u_{i}(\sigma _{i},\sigma _{{-i}})\ge u_{i}(\eta _{i},\sigma _{{-i}})$

Stwierdzenie 2.2

Strategia mieszana która dominuje każdą strategię czystą danego gracza, dominuje każdą strategię nieszaną tego gracza.

W szczególności strategia czysta która dominuje każdą inną strategię czystą danego gracza, dominuje każdą strategię nieszaną tego gracza. Dowód wynikający z liniowości wypłat, pomijamy.

Uwaga 2.5

Strategia ściśle zdominowana nie może wystepować w profilu równowagowym (”nie może być grana w równowadze”), gdyż gracz grający tą strategią mógłby podwyższyć swą wypłatę zmieniając ją na ścisle dominującą.

Usuwając ze zbioru strategii gracza strategię ściśle zdominowaną nie zmieniamy zbioru równowag Nasha. Jeżeli metoda eliminacji strategii ściśle zdominowanych prowadzi do jednego profilu gry, to jest on RN. Nie jest to prawda w przeciwną stronę - w wielu GS istnieją jednoznaczne RN które nie mogą być uzyskane tą metodą.

Uwaga 2.6

Algorytm usuwania strategii ściśle zdominowanych ( wynik nie zależy od kolejności usuwania):

1. Jeśli nie istnieje gracz który ma strategię ściśle zdominowaną, to stop. W przeciwnym razie przejdź do p. 2.

2. Usuń tę strategię i powróć do punktu 1.

Przykład 2.9

$\$

	L	S	R
U	4,3	5,1	6,2
M	2,1	8,4	3,6
D	3,0	9,6	2,8

Strategia R ściśle dominuje S, po usunięciu S strategia U ściśle dominuje M i D, po ich usunięciu L ściśle dominuje R. RN to profil (U,L).

Strategia czysta, jeśli nawet nie jest ścisle zdominowana przez żadną inną czystą, może być ściśle zdominowana przez mieszana, jak pokazuje

Przykład 2.10

$\$

	L	R
U	2,0	-1,0
M	0,0	0,0
D	-1,0	2,0

M nie jest ściśle zdominowana ani przez R ani D, natomiast jest ściśle zdominowana przez strategię $\sigma=(1/2,0,1/2)$ .

Stwierdzenie 2.3

Strategia która nie jest strategią czystą nie może być strategią ściśle dominującą.

Dowód pozostawiamy czytelnikowi jako ćwiczenie.

Ćwiczenie 2.1

Znależć wszystkie strategie słabo zdominowane i ściśle zdominowane w Słabym Dylemacie Więźnia.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Teorii Gier