Zagadnienia
6. Gry Bayesa
6.1. Uwagi wstępne
W dotychczas rozpatrywanym modelu gry strategicznej gracze którzy podejmowali decyzje mieli pełną informację dotyczącą gry, w szczególności znali macierze wypłat wszystkich graczy. W wielu rzeczywistych sytuacjach w ekonomii, w polityce, w konfliktach militarnych, w relacjach społecznych gracze mają zróznicowaną informację o pewnych aspektach gry, istotnych dla podjęcia decyzji o wyborze akcji. Gry w których przynajmniej jeden gracz posiada taka informację, tzn. nieznana conajmniej jednemu innemu graczowi, będziemy nazywać grami Bayesa (Bayesian games), albo grami z niepełną informacją. Używa się też terminu: gry z asymetryczną informacją.
W dotychczasowych rozważaniach dla GS gracze znali w szczególności akcje i wypłaty swoje i przeciwników. W rzeczywistych konfliktach często tak nie jest, walczący nie znaja siły przeciwników, firmy nie znaja kosztów produkcji konkurentów, uczestnicy aukcji nie znają waluacji obiektu aukcji przez innych uczestników aukcji. W grach opisujących takie sytuacje dochodzi więc element ryzyka związany z niepełną informacją.
W grach Bayesa definicja równowagi Nasha musi zostać zmieniona tak aby uwzględnić zróżnicowaną informację graczy o grze. Odpowiednie uogólnienie pojęcia równowagi będziemy nazywali równowagą Nasha–Bayesa, lub po prostu równowagą Bayesa. W takiej równowadze akcje graczy będa optymalne (będą najlepszymi odpowiedziami) przy ich określonych przekonaniach (beliefs) dotyczących innych graczy.
W formalnym modelu gry strategicznej uwzględniającym niepełną informację dojda dodatkowe obiekty–stany świata, i subiektywne, zależne od gracza prawdopodobieństwa wystąpienia różnych stanów świata. Odpowiednim modyfikacjom ulegną wypłaty, które będą wartościami oczekiwanymi odpowiednich zmiennych losowych, i w konsekwencji pojęcia najlepszej odpowiedzi.
Uwaga 6.1
Innym rodzajem niepełnej informacji o grze może być brak informacji gracza co inni gracze wiedzą o tym co wie dany gracz na temat gry. W grach ekstensywnych, będących tematem kolejnych rozdziałów, rozważa się jeszcze inny rodzaj niepewności w grze: brak pewności jaka akcję grał ostatnio przeciwnik (przeciwnicy). Gry tego typu nazwiemy grami z niedoskonałą informacją (imperfect information).
W poniższych przykładach (por. [19]) rozważymy gry dwuosobowe w których przynajmniej jeden gracz nie będzie miał pewności na temat wypłat swojego przeciwnika czy też partnera gry.
Przykład 6.2 (Duopol Cournota z asymetryczną informacją)
Niech ![]() jest funkcja kosztów 1-ej firmy. Funkcja kosztów 2-ej jest równa
jest funkcja kosztów 1-ej firmy. Funkcja kosztów 2-ej jest równa ![]() z prawdopodobieństwem
z prawdopodobieństwem ![]() ,
, ![]() z prawdopodobieństwem
z prawdopodobieństwem ![]() . Informacja graczy o grze jest asymetryczna w nastepującym sensie: 2 zna
. Informacja graczy o grze jest asymetryczna w nastepującym sensie: 2 zna ![]() and
and ![]() , 1 zna
, 1 zna ![]() i wie że koszt koszt wyprodukowania jednostki towaru przez firmę 2 wynosi
i wie że koszt koszt wyprodukowania jednostki towaru przez firmę 2 wynosi ![]() z prawdopodobieństwem
z prawdopodobieństwem ![]() ,
, ![]() z prawdopodobieństwem
z prawdopodobieństwem ![]() . Przykładowo, firma 2 może dopiero wchodzić na rynek lub wprowadzać nową technologię produkcji rozważanego towaru. Zakładamy ”common knowledge”: 1 wie co 2 wie o grze, 2 wie że 1 wie co 2 wie o grze itd.
. Przykładowo, firma 2 może dopiero wchodzić na rynek lub wprowadzać nową technologię produkcji rozważanego towaru. Zakładamy ”common knowledge”: 1 wie co 2 wie o grze, 2 wie że 1 wie co 2 wie o grze itd.
Przykład 6.3
Walka Płci (przy niepełnej informacji)
Rozważmy symetryczną GS: ![]() . 1-y gracz to Mężczyzna, 2-i gracz to Kobieta. B oznacza Boks, S–Siatkówkę. 1 and 2 muszą zdecydować jednocześnie: wybrać B czy S.
. 1-y gracz to Mężczyzna, 2-i gracz to Kobieta. B oznacza Boks, S–Siatkówkę. 1 and 2 muszą zdecydować jednocześnie: wybrać B czy S.
Gracz 1 ma macierz wypłat
| B | S | |
|---|---|---|
| B | 2 | 0 |
| S | 0 | 1 |
Gracz 2 może być jednym z dwóch typów: ![]() i
i ![]() (od ang.: love, hate). Gdy jest typu
(od ang.: love, hate). Gdy jest typu ![]() to jego macierz wypłat ma postać
to jego macierz wypłat ma postać
| B | S | |
|---|---|---|
| B | 1 | 0 |
| S | 0 | 2 |
a gdy typu ![]() , to
, to
| B | S | |
|---|---|---|
| B | 0 | 2 |
| S | 1 | 0 |
W tym przykładzie gracz 1 ma tylko jeden typ. Zakładamy że przy realizacji gry każdy gracz wie jakiego jest typu.
Gracz 1 nie wie z jakim typem gracza 2 będzie grał. Zakładając prawdopodobieństwo każdego typu równe (w naszym przykładzie) 0.5 i wiedząc jaką akcję wybierze (z prawdopodobieństwem 1) gracz 2 gdy jest każdego z typów, gracz 1 może obliczyć wypłaty ze swoich strategii czystych jako wartości oczekiwane zmiennej losowej ”typ gracza 2”.
Niech para (A,B) oznacza: gracz 2 gra A gdy jest typu ![]() , B gdy jest typu
, B gdy jest typu ![]() . Otrzymujemy macierz wartości oczekiwanych wypłat gracza 1 przy danych założeniach o graczu 2:
. Otrzymujemy macierz wartości oczekiwanych wypłat gracza 1 przy danych założeniach o graczu 2:
| (B,B) | (B,S) | (S,B) | (S,S) | |
|---|---|---|---|---|
| B | 2 | 1 | 1 | 0 |
| S | 0 | 1/2 | 1/2 | 1 |
Zauważmy że macierz tę można traktować jako macierz wypłat pewnej gry trzyosobowej.
Za profil strategii czystych gry przyjmiemy trójkę
Za profil rówowagowy (strategii czystych) przyjmiemy taki profil ![]() dla którego:
dla którego:
1. Przy ustalonych akcjach (A,B) 2-ego gracza gdy jest typu odpowiednio ![]() (i przy znanym graczowi 1 prawdopodobieństwie każdego typu gracza 2 (w maszym przykładzie 0.5) akcja
(i przy znanym graczowi 1 prawdopodobieństwie każdego typu gracza 2 (w maszym przykładzie 0.5) akcja ![]() daje graczowi 1 maksymalna wypłatę
daje graczowi 1 maksymalna wypłatę
2. Przy ustalonej akcji ![]() 1-ego: gdy 2-i jest typu
1-ego: gdy 2-i jest typu ![]() (typu
(typu ![]() ) to akcja
) to akcja ![]() (akcja
(akcja ![]() ) daje 2-emu maksymalna wypłatę.
) daje 2-emu maksymalna wypłatę.
Jak łatwo sprawdzić, w naszym przykładzie warunki te spełnia trójka ![]() .
.
6.2. Definicje
Definicja 6.3
Przekonanie (belief) ![]() gracza
gracza ![]() (o akcjach pozostałych graczy) jest to rozkład prawdopodobieństwa na
(o akcjach pozostałych graczy) jest to rozkład prawdopodobieństwa na ![]() .
.
Gracz ![]() jest racjonalny jeżeli wybiera strategię
jest racjonalny jeżeli wybiera strategię ![]() taką że
taką że
czyli taką która maksymalizuje wyrażenie
Przykładowo ![]() jest przekonaniem gracza 1 w grze koordynacyjnej
jest przekonaniem gracza 1 w grze koordynacyjnej
| C | D | |
|---|---|---|
| C | 1 | 0 |
| D | 0 | 1 |
Gracz 1 jest racjonalny jeżeli wybiera C.
Definicja 6.4
Niech ![]() będzie zbiorem skończonym. Elementy
będzie zbiorem skończonym. Elementy ![]() bedziemy nazywać stanami świata.
Przekonanie
bedziemy nazywać stanami świata.
Przekonanie ![]() gracza
gracza ![]() o stanach świata jest to rozkład prawdopodobieństwa na
o stanach świata jest to rozkład prawdopodobieństwa na ![]() .
.
Definicja 6.5
Gra Bayesowska
składa się z następujących elementów:
![]() – skończony zbiór graczy.
– skończony zbiór graczy.
![]() – skończony zbiór stanów świata.
– skończony zbiór stanów świata.
Dla każdego gracza ![]() określamy
określamy
-
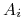 – zbiór akcji gracza
– zbiór akcji gracza 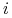 .
. -
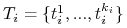 – skończony zbiór
– skończony zbiór 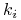 typów gracza
typów gracza 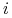 (sygnałów które może otrzymać).
W dalszym ciągu dla uproszczenia górny wskaźnik numerujący typ będziemy pomijać.
(sygnałów które może otrzymać).
W dalszym ciągu dla uproszczenia górny wskaźnik numerujący typ będziemy pomijać.
-
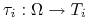 – funkcja sygnału gracza
– funkcja sygnału gracza 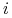 . Przyporządkowuje ona stanom świata typ gracza
. Przyporządkowuje ona stanom świata typ gracza 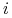 .
.Moc zbioru stanów które generują ryp
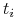 opisuje stopień pewności gracza
opisuje stopień pewności gracza 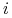 o stanie świata. Na przykład
jeżeli
o stanie świata. Na przykład
jeżeli 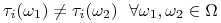 to gracz
to gracz 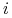 wie, po otrzymaniu sygnału, jaki jest stan świata (jaki stan ”zaszedł”), a zatem zna typy wszystkich graczy.
wie, po otrzymaniu sygnału, jaki jest stan świata (jaki stan ”zaszedł”), a zatem zna typy wszystkich graczy.Jeżeli natomiast
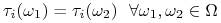 to sygnął który otrzymuje gracz (a zatem jego typ) nie daje mu żadnej informacji o stanie świata.
to sygnął który otrzymuje gracz (a zatem jego typ) nie daje mu żadnej informacji o stanie świata.W pozostałych przypadkach informacja ma charakter częściowy. Niech np. świat ma trzy stany:
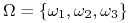 ,
, 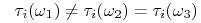 . Jeżeli świat jest w stanie
. Jeżeli świat jest w stanie 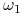 , to gracz
, to gracz 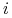 wie że świat jest w stanie
wie że świat jest w stanie 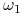 , jesli
, jesli 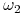 lub
lub 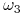 to gracz
to gracz 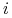 nie wie w którym z tych stanów.
nie wie w którym z tych stanów. -
Dla każdego typu
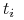
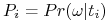 jest prawdopodobieństwem apriori (prior belief) jakie typ
jest prawdopodobieństwem apriori (prior belief) jakie typ 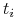 assigns stanowi
assigns stanowi 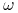 .
.Funkcja sygnału
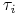 wraz ze zbiorem prawdopodobieństw apriori opisują wiedzę
wraz ze zbiorem prawdopodobieństw apriori opisują wiedzę 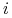 o stanie świata.
o stanie świata. -
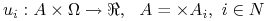 – funkcja wypłat gracza
– funkcja wypłat gracza 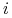 .
.
Gra odbywa się w następstwie realizacji pewnego stanu świata ![]() .
.
Gracz ![]() otrzymuje sygnał (dla uproszczenia oznaczeń pomijamy numer sygnału)
otrzymuje sygnał (dla uproszczenia oznaczeń pomijamy numer sygnału) ![]() , czyli jest typu
, czyli jest typu ![]() . Typ
. Typ ![]() definiuje podzbiór stanów świata
definiuje podzbiór stanów świata ![]() (które implikują typ
(które implikują typ ![]() ).
Dla każdego takiego stanu
).
Dla każdego takiego stanu ![]() otrzymujemy
otrzymujemy ![]() - aprioryczne prawdobodobieństwa gracza
- aprioryczne prawdobodobieństwa gracza ![]() w stanie
w stanie ![]() że stan świata jest
że stan świata jest ![]() . Mając te prawdopodobieństwa obliczamy wypłaty gracza
. Mając te prawdopodobieństwa obliczamy wypłaty gracza ![]() .
.
Przykład 6.4
W rozpatrywanej grze Walka Płci (przy niepełnej informacji):
![]()
![]()
![]()
Funkcje sygnału: gracza 1: ![]() – gracz 1 może otrzymać tylko jeden sygnał, jest tylko jednego typu.
– gracz 1 może otrzymać tylko jeden sygnał, jest tylko jednego typu.
gracza 2: ![]() – gracz 2 może być typu
– gracz 2 może być typu ![]() lub typu
lub typu ![]() .
.
Prawdopodobieństwa aprioryczne gracza 1:
Mówimy że gracz ![]() przypisuje każdemu stanowi świata prawdopodobieństwo 1/2 po otrzymaniu sygnału
przypisuje każdemu stanowi świata prawdopodobieństwo 1/2 po otrzymaniu sygnału ![]() .
.
Prawdopodobieństwa aprioryczne gracza 2:
Gracz ![]() przypisuje prawdopodobieństwo 1 stanowi
przypisuje prawdopodobieństwo 1 stanowi ![]() po otrzymaniu synału
po otrzymaniu synału ![]() i stanowi
i stanowi ![]() po otrzymaniu sygnału
po otrzymaniu sygnału ![]() .
.
Wypłaty: dla ![]() :
:
Liczby ![]() są elementami macierzy wypłat gdy 2 jest typu
są elementami macierzy wypłat gdy 2 jest typu ![]() ,
,
Liczby ![]() są elementami macierzy wypłat gdy 2 jest typu
są elementami macierzy wypłat gdy 2 jest typu ![]() .
.
Definicja 6.6
Równowaga Nasha Gry Bayesowskiej GB jest to RN następującej GS:
Gracze: pary ![]() , gdzie
, gdzie ![]()
Zbiór akcji gracza ![]() jest to zbiór akcji
jest to zbiór akcji ![]() gracza
gracza ![]() w GS
w GS
Wypłaty gracza ![]() definiujemy następująco:
definiujemy następująco:
Oznaczmy: ![]() –akcja typu
–akcja typu ![]() gracza
gracza ![]() .
.
Wypłata gracza ![]() wybierającego akcję
wybierającego akcję ![]() jest równa
jest równa
![]() jest profilem GS w której gracz
jest profilem GS w której gracz ![]() typu
typu ![]() gra
gra ![]() , a pozostali grają
, a pozostali grają ![]() ,
, ![]() jest wprowadzonym wyżej oznaczeniem akcji gracz
jest wprowadzonym wyżej oznaczeniem akcji gracz ![]() typu
typu ![]() gdy stan świata jest
gdy stan świata jest ![]() .
.
Zauważmy że ![]() zależy od akcji wszystkich typów wszystkich pozostałych graczy, a nie zależy od akcji żadnego z typów gracza
zależy od akcji wszystkich typów wszystkich pozostałych graczy, a nie zależy od akcji żadnego z typów gracza ![]() .
.
6.3. Przykłady
Przykład 6.5
W rozważanym wyżej Przykładzie 6.4 policzymy oczekiwaną wypłatę (jedynego) typu ![]() gracza 1 z akcji
gracza 1 z akcji ![]() , gdy
, gdy ![]() :
:
Przykład 6.6 (Battle of the Sexes (with incomplete information))
Niech obaj gracze mogą być jednego z dwóch typów: ![]() , i że nie wiedzą jakiego typu jest przeciwnik: 1 przypisuje typowi 2-go prawdopodobieństwo 1/2, 2-i przypisuje 1-mu typ
, i że nie wiedzą jakiego typu jest przeciwnik: 1 przypisuje typowi 2-go prawdopodobieństwo 1/2, 2-i przypisuje 1-mu typ ![]() z prawdopodobieństwem 2/3,
z prawdopodobieństwem 2/3, ![]() z prawdopodobieństwem 1/3. Gracze znają swoje typy.
z prawdopodobieństwem 1/3. Gracze znają swoje typy.
Tę sytuację modelujemy jako następującą GB:
![]()
![]()
Funkcja sygnału gracza 1: ![]()
Funkcja sygnału gracza 2: ![]()
Prawdopodobieństwa aprioryczne (beliefs) gracza 1:
Prawdopodobieństwa aprioryczne (beliefs) gracza 2:
Wypłaty: dla ![]() : liczby
: liczby ![]() są elementami macierzy
są elementami macierzy ![]() .
.
![]() :
:
| B | S | |
|---|---|---|
| B | 2,1 | 0,0 |
| S | 0,0 | 1,2 |
![]() :
:
| B | S | |
|---|---|---|
| B | 2,0 | 0,2 |
| S | 0,1 | 1,0 |
![]() :
:
| B | S | |
|---|---|---|
| B | 0,1 | 2,0 |
| S | 1,0 | 0,2 |
![]() :
:
| B | S | |
|---|---|---|
| B | 0,0 | 2,2 |
| S | 1,1 | 0,1 |
Przykład 6.7 (Duopol Cournota z asymetryczną informacją)
![]()
W Przykładzie 6.2 gra Bayesa ma postać:
![]() ,
, ![]() ,
, ![]() .
.
Funkcje sygnału: ![]() .
.
Prawdopodobieństwa aprioryczne: jedyny typ gracza 1 przypisuje prwadopodobieństwo ![]() stanowi
stanowi ![]() ,
, ![]() stanowi
stanowi ![]() . Każdy typ gracza 2 przypisuje prawdopodobieństwo 1 każdemu stanowi konsystentnemu ze swoim sygnałem
. Każdy typ gracza 2 przypisuje prawdopodobieństwo 1 każdemu stanowi konsystentnemu ze swoim sygnałem ![]() , natomiast prawdopodobieństwo
, natomiast prawdopodobieństwo ![]() w przeciwnym przypadku.
w przeciwnym przypadku.
Funkcje wypłaty: ![]() gdzie
gdzie ![]() , a
, a ![]() jest rynkową ceną jednostki towaru którego całkowita produkcja wynosi
jest rynkową ceną jednostki towaru którego całkowita produkcja wynosi ![]() .
.
Ćwiczenie 6.1
![]()
W duopolu Cournota z Przykładu 9.7 dla ![]() dostatecznie bliskich by istniała RN z dodatnimi produkcjami znaleźć tę RN i porównać z RN gier w których 1 zna
dostatecznie bliskich by istniała RN z dodatnimi produkcjami znaleźć tę RN i porównać z RN gier w których 1 zna ![]() i
i ![]() .
.
Niech ![]() dla
dla ![]() ,
, ![]() dla
dla ![]() . Niech
. Niech ![]() – RN. Wtedy
– RN. Wtedy
![]()
![]() .
.
Obliczając pierwsze pochodne otrzymujemy 3 równania algebraiczne na ![]() . Ich rozwiązanie:
. Ich rozwiązanie:
Przypomnijmy że dla duopolu Cournota z pełną informacją gdy koszt produkcji firmy ![]() wynosi
wynosi ![]() , to zakładając dodatniość odpowiednich wielkości produkcji, w RN wielkości te wynoszą
, to zakładając dodatniość odpowiednich wielkości produkcji, w RN wielkości te wynoszą
W szczególoności otrzymujemy więc
Przykład 6.9 (Nadmiar informacji może obniżyć wypłatę)
![]()
I. Rozważmy wpierw 2-osobową GB z dwoma stanami: ![]() , w której żaden z graczy nie zna stanu świata i każdy przypisuje prawdopodobieńtwo 1/2 każdemu z 2 stanów. Macierze wypłat odpowiadające obu stanom mają postać:
, w której żaden z graczy nie zna stanu świata i każdy przypisuje prawdopodobieńtwo 1/2 każdemu z 2 stanów. Macierze wypłat odpowiadające obu stanom mają postać:
![]() :
:
| L | M | R | |
|---|---|---|---|
| T | 1,2a | 1,0 | 1,3a |
| B | 2,2 | 0,0 | 0,3 |
![]() :
:
| L | M | R | |
|---|---|---|---|
| T | 1,2a | 1,3a | 1,0 |
| B | 2,2 | 0,3 | 0,0 |
gdzie ![]() .
.
Najlepsza odpowiedź gracza 2 na każdą akcję 1-go to L:
jeśli 1 wybierze T, to L da 2a, M i R dadzą po 3a/2 każda.
jeśli 1 wybierze B, to L da 2, M i R dadzą po 3/2 każda.
Co więcej, najlepsza odpowiedź 1 na L to B. Ponieważ jest to jedyna najlepsza odpowiedż, więc para (par) ![]() jest jedyną RN (także w strategiach mieszanych). W Rn każdy gracz otrzymuje 2.
jest jedyną RN (także w strategiach mieszanych). W Rn każdy gracz otrzymuje 2.
II. Rozważmy teraz nastepującą modyfikację tej gry. Gracz 2 zna stan świata: ![]() . Mamy sytuację taką jak w pierwszej wersji gry Wojna Płci z niepełną informacja. Gracz 2 ma więc więcej informacji. Zakładamy że gracz 1 jest o tym poinformowany.
. Mamy sytuację taką jak w pierwszej wersji gry Wojna Płci z niepełną informacja. Gracz 2 ma więc więcej informacji. Zakładamy że gracz 1 jest o tym poinformowany.
W tej grze ![]() jest jedyną RN: każdy typ gracza 2 ma strategię ścisle dominującą, wprzy której jedyną najlepszą odpowiedzią gracza 1 jest T. W tej RN gracz 2 otrzymuje
jest jedyną RN: każdy typ gracza 2 ma strategię ścisle dominującą, wprzy której jedyną najlepszą odpowiedzią gracza 1 jest T. W tej RN gracz 2 otrzymuje ![]() w każdym ze stanów, a więc wypłatę niższą niż w przypadku I!
w każdym ze stanów, a więc wypłatę niższą niż w przypadku I!




