Zagadnienia
9. Gry Ekstensywne I
9.1. Wprowadzenie
Inne używane nazwy: Gry w postaci ekstensywnej, Gry w postaci rozwiniętej, Gry Dynamiczne. (EG: Extensive Games, Games in Extensive Form, Sequential Move(s) Game). Będziemy używać skrótu GE.
W GS gracze podejmują decyzje jednocześnie, lub nie znając decyzji przeciwników. W GE gracze podejmują decyzje sekwencyjnie, następstwo czasowe odgrywa kluczową rolę.
Wiele sytuacji politycznych, ekonomicznych, społecznych, (np. aukcje, wspołzawodnictwo firm wprowadzających nowe technologie, negocjacje cenowe, jak równiez wiele gier towarzyskich można opisać jako gry ekstensywne.
Jeżeli nie będzie powiedziane inaczej, będziemy zakładać że gracze są w pełni racjonalni, tzn. jedynym kryterium wyboru ich strategii są wypłaty (ogólniej - preferencje) - gracze maksymalizują swoje wypłaty i nie popełniają błędów przy wyborze strategii.
Wpierw zajmiemy się GE z pełną (kompletną) informacja (EG of (with) Complete Information, EG of (with) Perfect Information), tzn. GE w których:
1: w każdej chwili (w każdym kroku czasowym) dokładnie jeden gracz podejmuje decyzję (jaką akcję wybiera),
2: każdy gracz zna cały dotychczasowy przebieg gry (wie który gracz jaką decyzję podjął w poprzednich chwilach w których podejmował decyzję).
3. powyższa informacja jest wspólną wiedzą (common knowledge).
Przykład 9.1
Ultimatum, Gra w Stonogę patrz Wykład I.
Przykład 9.2
Firma F może wynająć (W) lub nie (N) robotnika (R). Jeśli N to F i P mają wypłaty 0. Jeżeli W, to R może pracować (P) (i wtedy obaj gracze dostaja po 1), lub nie (L), co daje -1 dla F i 2 dla R.
Przykład 9.3 (Gra na Wejście (Odstraszanie) Entry Deterrence Game)
Firma F (pretendent, intruz) ma podjąć decyzję czy wejść (In) czy nie (Out) na rynek monopolisty M incumbent (broniacy, właściciel). F ma wartość 1, M ma wartość 2. Jeśli F wybierze Out to wypłaty graczy są równe ich wartościom. Jeśli F wybierze In to M ma do wyboru dwie akcje: Agree, z wypłatą 2 dla F i 1 dla M, lub Fight, z wypłatą 0 dla F i 0 dla M.
Podstawowe elementy GE to zbiór graczy, kolejność ich ruchów, zbiory akcji każdego gracza gdy jest jego ruch, wyniki gry, preferencje graczy na wynikach. Wszystkie te elementy GE opisuje drzewo (wykres, diagram, graf) gry (game tree). Drzewo gry składa się z
-
węzłów (wierzchołków).
-
gałęzi
-
zbiorów informacyjnych.
-
indykatorów graczy
-
indykatorow akcji
-
wypłat
Definicja 9.1
GE w których wszystkie zbiory informacyjne są singletonami i w których gracze znają wszystkie poprzednie grane akcje i graczy którzy je wykonywali nazywamy GE z doskonałą (zupełną, pełną, kompletną) informacją.
Uwaga 9.1
Jeśli gracze znają wszystkie poprzednie grane akcje i graczy którzy je wykonywali to mówimy że mają doskonałą pamięć (perfect recall). Na ogół zakłada się że to zachodzi (wpp. trudno o rozsądną koncepcję równowagi, czy też rozwiązania gry–trudno pogodzić racjonalność graczy i ich niedoskonałą pamięć…).
9.2. Definicja GE z Doskonałą Informacją
Pełna nazwa gier omawianych w tym rozdziale: Gry Ekstensywne z Doskonałą Informacją . Bedziemy używali w tym rozdziale skrótu: Gry Ekstensywne. Później omówimy krótko GE z Niedoskonałą Informacją.
Definicja 9.2
Gra Ekstensywna jest to czwórka ([18])
-
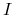 - zbiór graczy
- zbiór graczy -
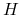 - zbiór historii – zbiór ciagów (skończonych lub nieskończonych) t. że
- zbiór historii – zbiór ciagów (skończonych lub nieskończonych) t. żea) jeżeli ciąg
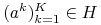 (
(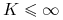 ) oraz
) oraz 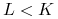 to
to 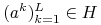
b) jeżeli ciąg
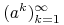 spełnia
spełnia 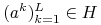
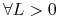 to
to 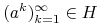
Dodatkowo
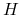 zawiera pewien element,
zawiera pewien element, 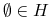 , nazywany ”ciągiem pustym”
. Jest on potrzebny by zdefiniować ”poczatek gry”, patrz niżej.
, nazywany ”ciągiem pustym”
. Jest on potrzebny by zdefiniować ”poczatek gry”, patrz niżej.Elementy zbioru
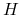 oznaczamy
oznaczamy 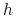 i nazywamy historiami. Wyrazy każdego (niepustego) ciągu
(niepustej historii) są elementami pewnego zbioru
i nazywamy historiami. Wyrazy każdego (niepustego) ciągu
(niepustej historii) są elementami pewnego zbioru 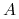 , nazywanego zbiorem akcji. Nazywamy je akcjami (graczy).
, nazywanego zbiorem akcji. Nazywamy je akcjami (graczy).Potocznie mówimy: Historia jest ciągiem akcji (lub jest pusta).
Historia
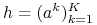 jest zakończona (terminal) jeśli jest ciągiem nieskończonym (mówimy: jest nieskończona),
lub jeśli nie istnieje akcja
jest zakończona (terminal) jeśli jest ciągiem nieskończonym (mówimy: jest nieskończona),
lub jeśli nie istnieje akcja 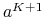 t. że
t. że 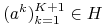 .
Zbiór historii zakończonych oznaczamy
.
Zbiór historii zakończonych oznaczamy 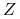 .
. -
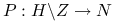 - indykator gracza, funkcja gracza (player function).
- indykator gracza, funkcja gracza (player function).
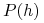 zwraca numer gracza który podejmuje decyzję (wykonuje ruch) po historii
zwraca numer gracza który podejmuje decyzję (wykonuje ruch) po historii 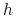 .
. -
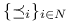 - zbiór relacji preferencji na zbiorze
- zbiór relacji preferencji na zbiorze 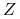 .
. 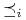 jest relacją preferencji gracza
jest relacją preferencji gracza 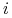 na zbiorze
na zbiorze 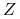 .
.Na zakończonych historiach definiujemy preferencje graczy przez podanie funkcji wypłat które opisują te preferencje (zgodnych z tymi preferencjami):
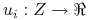 .
.
Definicja 9.3
GE jest skończona jeżeli zbiór ![]() jest skończony.
GE ma skończony horyzont jeżeli najdłuższa historia jest skończona.
Niekiedy warunek skończoności horyzontu jest częścią definicji gry skończonej.
jest skończony.
GE ma skończony horyzont jeżeli najdłuższa historia jest skończona.
Niekiedy warunek skończoności horyzontu jest częścią definicji gry skończonej.
Uwaga 9.3
Gra która nie jest skończona może mieć skończony horyzont. Przykład - Gra Ultimatum z przeliczalną (lub continuum) liczba ofert.
Uwaga 9.4
Definicja GE nie precyzuje zbioru akcji gracza gdy jest jego ruch (po historii ![]() ). Zbiór ten można odtworzyć ze zbioru
). Zbiór ten można odtworzyć ze zbioru ![]() zakończonych historii i funkcji gracza
zakończonych historii i funkcji gracza ![]() w następujący sposób.
w następujący sposób.
Jeśli dla ![]() ciąg
ciąg ![]() (tzn. jest historią), to akcja
(tzn. jest historią), to akcja ![]() jest jedną z akcji którą może grać gracz
jest jedną z akcji którą może grać gracz ![]() po historii
po historii ![]() . Zbiór takich akcji oznaczamy
. Zbiór takich akcji oznaczamy ![]() . Formalnie:
. Formalnie:
Definicja 9.4 (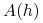 –zbiór akcji gracza
–zbiór akcji gracza 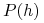 po historii
po historii 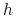 )
)
:
gdzie ![]() oznacza zbiór wszystkich wyrazów ciągów występujących w
oznacza zbiór wszystkich wyrazów ciągów występujących w ![]() , identyfikowany ze zbiorem wszystkich akcji wszystkich
graczy .
, identyfikowany ze zbiorem wszystkich akcji wszystkich
graczy .
Opis przebiegu gry:
Gra zaczyna sie od historii pustej ![]() . Liczba
. Liczba ![]() jest numerem gracza który pierwszy wykonuje ruch -
wybiera akcję
jest numerem gracza który pierwszy wykonuje ruch -
wybiera akcję ![]() ze zbioru
ze zbioru ![]() , która wyznacza historię
, która wyznacza historię ![]() .
.
Uwaga 9.5
W dalszym ciagu będziemy w historiach niepustych pomijać symbol ![]() , czyli np. historię
, czyli np. historię ![]() oznaczamy
oznaczamy ![]() , lub jeszcze krócej, symbolem
, lub jeszcze krócej, symbolem ![]() .
.
Jeśli historia ![]() to gra się kończy,
wpp. znajdujemy
to gra się kończy,
wpp. znajdujemy ![]() . Gracz
. Gracz ![]() wybiera akcję ze zbioru
wybiera akcję ze zbioru ![]() . Ten wybór wyznacza następnego gracza. Ogólnie:
Niech
. Ten wybór wyznacza następnego gracza. Ogólnie:
Niech ![]() - historia o długości
- historia o długości ![]() . Jeśli
. Jeśli ![]() to gra się kończy. Wpp. gracz
to gra się kończy. Wpp. gracz ![]() wybiera akcję ze zbioru
wybiera akcję ze zbioru ![]() ,
aż uzyskamy historię zakończoną. .
,
aż uzyskamy historię zakończoną. .
Przykład 9.4
W Grze na Wejście:
![]()
Przebieg gry:
![]() (Firm, player 1)
(Firm, player 1)
![]()
Z tego zbioru gracz ![]() wybiera akcję
wybiera akcję ![]() która wyznacza historię
która wyznacza historię ![]() .
Jeśli
.
Jeśli ![]() to gra się kończy (indykator gracza nie jest określony na
to gra się kończy (indykator gracza nie jest określony na ![]() ).
Jeśli
).
Jeśli ![]() to obliczamy
to obliczamy ![]() , oraz
, oraz
Preferencje graczy na zakończonych historiach ustalamy w następujący sposób :
Wprowadzamy funkcje wypłat zgodne z tymi preferencjami:
9.3. Strategie w GE
W GE podstawową rolę będzie odgrywało pojęcie strategii. Strategia gracza to przepis, algorytm, którą akcję ma wybrać w każdej chwili w której w której przypada jego ruch, czyli kompletny plan akcji ”na całą grę”, na wszystkie możliwe sytuacje w grze. Akcja gracza (decyzja, wybór, ruch, posunięcie) to element ze zbioru akcji gracza. Strategia gracza w GE określa przede wszystkim akcję gracza po każdej historii po której jest jego ruch.
Formalne definicje będą podane niżej.
.
Przykład 9.5
Pieszy ma 2 akcje: może na światłach przejść przez jezdnię (P) lub nie (N), the światła mogą być C, Ż lub Z.
Strategie pieszego to wektory ![]() ,
, ![]() jest akcją jeśli R,
jest akcją jeśli R, ![]() - jeśli Ż,
- jeśli Ż,
![]() - jeśli Z. Pieszy ma
- jeśli Z. Pieszy ma ![]() strategii. Na przykład
strategii. Na przykład ![]() - nieuważanie,
- nieuważanie, ![]() - pasywna,
- pasywna,
![]() - postępuj zgodnie z prawem,
- postępuj zgodnie z prawem, ![]() - szalona1,
- szalona1, ![]() - szalona2 itd.
- szalona2 itd.
Przykład 9.6
Jeżeli partia szachów kończyłaby się po pierwszym ruchu czarnych to białe miałyby ![]() strategii, a czarne
strategii, a czarne ![]() strategii.
W ”jednoruchowej” grze w GO (bez handicapów) białe mają
strategii.
W ”jednoruchowej” grze w GO (bez handicapów) białe mają ![]() , a czarne
, a czarne ![]() strategii.
strategii.
Gra Kółko i krzyżyk (noughts and crosses). Gracz 1 (np. ”kółkowy”) ma w 1-ym ruchu 9 akcji. Gracz 2 ma w swym 1-ym ruchu 8 akcji. Jeżeli gra kończyłaby się po 1-ym ruchu gracza 2 to ma on ![]() strategii. Jeżeli po 2-im ruchu gracza 1 to w takiej grze gracz 1 ma
strategii. Jeżeli po 2-im ruchu gracza 1 to w takiej grze gracz 1 ma ![]() strategii.
strategii.
Do formalnej definicji strategii będzie nam potrzebna
Definicja 9.5 (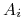 - zbiór (wszystkich) akcji gracza
- zbiór (wszystkich) akcji gracza 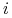 )
)
Uwaga 9.6
W powyższej definicji zamiast ![]() można napisać
można napisać ![]() .
.
Dla ![]() definiujemy
definiujemy
Definicja 9.6 (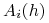 - zbiór akcji gracza
- zbiór akcji gracza 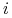 po historii
po historii 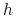 )
)
Definicja (ważna) 9.7
Strategia gracza ![]() w GE jest to funkcja
w GE jest to funkcja
W pewnym sensie definicja strategii jest ”nadokreślona” , może specyfikować akcje które nie będą grane jeżeli były grane wcześniej inne akcje determinowane przez daną strategie (Przykład 9.8 poniżej). Taka definicja jest potrzebna do sformułowania pojęcia równowagi (Nasha) w grach ekstensywnych, a następnie równowagi doskonałej ze względu na podgry.
Przykład 9.7
Targ (Bargaining Game) Gracz 1 (Klient) ocenia wartość przedmiotu sprzedawanego przez gracza 2 (Sprzedawca) na 600. Przedmiot ma dla gracza 2 wartość 50. Gracz 1 może złożyć dwie oferty: zapłaci 100 (C) lub 500 (D). Gracz 2 może w przypadku każdej z ofert zgodzić się na sprzedaż (E w przypadku oferty C, G w przypadku oferty D) lub nie (F w przypadku oferty C, H w przypadku oferty D). Akcja E implikuje wypłaty (”czyste zyski”) graczy: (500, 50), gdzie pierwszy element oznacza wypłatę gracza 1, oferta F implikuje wypłaty (0,0), G: (100, 450), H: (0,0). W tej GE:
![]()
![]() gdzie
gdzie ![]() - ciągi jednowyrazowe.
- ciągi jednowyrazowe.
Strategie gracza 2 to funkcje ![]() , takie że
, takie że
gdzie
Tak więc ![]() a zatem gracz 2 ma 4 strategie:
a zatem gracz 2 ma 4 strategie:
Strategie gracza 1 to funkcje ![]() , takie że
, takie że
gdzie
Ma być ![]() a zatem gracz 1 ma dwie strategie:
a zatem gracz 1 ma dwie strategie: ![]() :
:
Oznaczamy je ![]() , w odróżnieniu od niezakończonych historii
, w odróżnieniu od niezakończonych historii ![]() .
.
W powyższym przykładzie strategia gracza może być opisana jako ”plan akcji na wszystkie sytuacje”. W ogólności strategia ma ogólniejsze znaczenie.
Przykład 9.8
![]() . Niech
. Niech ![]() Jeśli gracz 1 gra D to otrzymujemy historię zakończoną (”gra się kończy”),
wypłaty graczy to (2,0), gdzie pierwszy element oznacza wypłatę gracza 1. Jeśli 1 gra C,
to określamy
Jeśli gracz 1 gra D to otrzymujemy historię zakończoną (”gra się kończy”),
wypłaty graczy to (2,0), gdzie pierwszy element oznacza wypłatę gracza 1. Jeśli 1 gra C,
to określamy ![]() czyli ma ruch gracz 2. Gracz 2-i ma do wyboru dwie akcje: E i F. Jeśli zagra F to gra się kończy i
wypłaty są (3,1), jeśli zagra E to otrzymujemy historię niezakończoną
czyli ma ruch gracz 2. Gracz 2-i ma do wyboru dwie akcje: E i F. Jeśli zagra F to gra się kończy i
wypłaty są (3,1), jeśli zagra E to otrzymujemy historię niezakończoną ![]() , z
, z ![]() , po której gracz 1-y ma do
wyboru dwie akcje: G i H. Jeśli zagra G to wypłaty są (1,2), jeśli H to wypłaty są (0,0). W obu przypadkach gra się kończy.
, po której gracz 1-y ma do
wyboru dwie akcje: G i H. Jeśli zagra G to wypłaty są (1,2), jeśli H to wypłaty są (0,0). W obu przypadkach gra się kończy.
Gracz 1 ma ruch po historii ![]() i po
i po ![]() (pomijamy w oznaczeniach historii niepustych symbol
(pomijamy w oznaczeniach historii niepustych symbol ![]() ).
).
Każda strategia gracza 1 to funkcja:
czyli, pamiętając że ![]() ,
,
Takich funkcji jest 4, więc gracz 1 ma 4 strategie ![]() , oznaczane kolejno
, oznaczane kolejno ![]() :
:
CG: wybierz C po historii ![]() i G po (C,E)
i G po (C,E)
CH: wybierz C po historii ![]() i H po (C,E)
i H po (C,E)
DG: wybierz D po historii ![]() i G po (C,E)
i G po (C,E)
DH: wybierz D po historii ![]() i H po (C,E).
i H po (C,E).
Gracz 2 ma dwie strategie, ![]() , które oznaczymy E, F – tak jak jego akcje.
, które oznaczymy E, F – tak jak jego akcje.
Przedstawiona formalizacja będzie potrzebna do podanej niżej definicji postaci strategicznej gry ekstensywnej i do zdefiniowania, w nastepnym wykładzie, równowagi Nasha w GE.
Definicja 9.8
Profil strategii w GE jest to wektor ![]() , gdzie
, gdzie ![]() - strategia gracza
- strategia gracza ![]() .
.
Definicja 9.9
Wynik ![]() GE z profilu
GE z profilu ![]() jest to zakończona
historia
jest to zakończona
historia ![]() skonstruowana nastepujący sposób.
skonstruowana nastepujący sposób.
Gracz ![]() stosuje strategię
stosuje strategię ![]() z profilu
z profilu ![]() , grając akcję
, grając akcję
która definiuje historię ![]() . Jeżeli
. Jeżeli ![]() to oznaczamy ją
to oznaczamy ją ![]() i nazywamy wynikiem
i nazywamy wynikiem ![]() GE
z profilu
GE
z profilu ![]() (outcome of the profile
(outcome of the profile ![]() ). Jeżeli
). Jeżeli ![]() to gracz
to gracz ![]() stosując swoją strategię
stosując swoją strategię ![]() z profilu
z profilu ![]() gra akcję
gra akcję
Jeśli historia ![]() , to proces kontynuujemy aż do otrzymania historii zakończonej.
Oznaczamy ją
, to proces kontynuujemy aż do otrzymania historii zakończonej.
Oznaczamy ją ![]() i nazywamy wynikiem GE z profilu
i nazywamy wynikiem GE z profilu ![]() . Formalnie:
. Formalnie:
Definicja 9.10
Wynik ![]() GE z profilu strategii
GE z profilu strategii ![]() jest to zakończona historia
jest to zakończona historia
taka że
Zapis ten oznacza że po ”podhistorii” ![]() historii
historii ![]() jest grana akcja
jest grana akcja
![]() przez gracza
przez gracza
![]() który stosuje strategię
który stosuje strategię ![]() z profilu
z profilu ![]() . Akcja
. Akcja ![]() jest wyznaczona jednoznacznie przez strategię
jest wyznaczona jednoznacznie przez strategię
![]() z profilu
z profilu ![]() . Zauważmy że
. Zauważmy że ![]() jest, z konstrukcji, jednoznacznie wyznaczony przez
jest, z konstrukcji, jednoznacznie wyznaczony przez ![]() .
.
9.4. Postać Strategiczna GE
Rozważmy ![]() .
Każda GE indukuje pewną GS, którą będziemy nazywać Postacią Strategiczną GE
(strategic form, normal form representation of EG).
.
Każda GE indukuje pewną GS, którą będziemy nazywać Postacią Strategiczną GE
(strategic form, normal form representation of EG).
Definicja 9.11
Postać Strategiczna GE ![]() jest to GS:
jest to GS: ![]() w której
w której
-
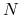 - zbiór graczy GE;
- zbiór graczy GE; 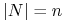 .
. -
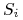 - zbiór akcji gracza
- zbiór akcji gracza 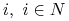 , jest to zbiór jego strategii w GE.
, jest to zbiór jego strategii w GE. -
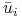 - funkcja wypłat gracza
- funkcja wypłat gracza 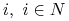 . Wypłata
. Wypłata 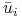 z danego profilu akcji
z danego profilu akcji 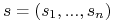 jest równa wypłacie
jest równa wypłacie 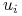 gracza
gracza 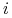 z wyniku
z wyniku 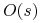 GE generowanego przez profil
GE generowanego przez profil 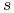 w GE. Formalnie
w GE. Formalnie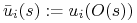
Uwaga 9.7
Uwaga: W dalszym ciągu będziemy dla uproszczenia utożsamiali ![]() .
.
Przykład 9.10
W Grze na Wejście:
F ma strategie In, Out, M ma strategie Agree, Fight. Postać strategiczna tej GE to GS o macierzy wypłat:
| Agree | Fight | |
|---|---|---|
| In | 2,1 | 0,0 |
| Out | 1,2 | 1,2 |
Przykład 9.11
Macierz wypłat Postaci Strategicznej GE ”Targ” z przykładu 9.7:
| EG | EH | FG | FH | |
|---|---|---|---|---|
| C | 500,50 | 500,50 | 0,0 | 0,0 |
| D | 100,450 | 0,0 | 100,450 | 0,0 |
Przykład 9.12
Macierz wypłat Postaci Strategicznej GE z przykładu 9.8:
| E | F | ||||
|---|---|---|---|---|---|
| CG | 1,2 | 3,1 | |||
| CH | 0,0 | 3,1 | |||
| DG | 2,0 | 2,0 | |||
| DH | 2,0 | 2,0 |




